Menu Close

Crash Course JC1 H2 Math

Emily

Here, you’ll find a H2 Math crash course on the topics learned in JC1.

Topics Covered in H2 Math

Here are H2 Math Topics that typically covered in JC1. There’s some slight variations among different schools, but theses are the topics most schools cover in JC1:

Click on the link to each of the topic above to go to the quick crash course on the topic.

System of Linear Equations

Systems of linear equation is often the first chapter that is learned in H2 Math in JC1.

A system of linear equations consist of 2 or more linear equations. Linear equations are equations where the unknown variable has a power of 1. Questions from this chapter often involves solving a system of linear equation with 3 or 4 unknowns.

Here’s an example of a system of linear equation:

3x+y-z=5

2x+y+z=2

x-2y+2z=1

The solution for this system of linear equation is: x = 11/7, y= -3/7, z = -5/7

The use of the graphic calculator (APPS –> Polysmlt) is used to solve the questions. –> Go here to learn step-by-step on how to use GC to solve systems of linear equation.

Note that in order to solve for n unknowns, you’ll need n equations.

Inequalities

There are 2 ways to solve inequalities:

  • without calculator (i.e. mathematically)
  • graphically using the graphic calculator (G.C)

Solving Inequalities without the calculator

Before you move on to the inequality, make sure you are familiar with the rules of inequalities, and also how to solve quadratic inequalities (you’ve learned this in O Level Additional Math). Once you are familiar with these topics learned in secondary school, here are the new concepts that you’ll learn:

Solving Inequalities graphically using the G.C

This involves using the graph function on the graphic calculator, and determine which range of values of x satisfy the inequality. Read here for detailed explanation.

Curve Sketching

In curve sketching, you’ll need to use the graphic calculator A LOT, to sketch the graph. You’ll be tested on sketching graphs written in cartesian form (i.e. y in term of x, or x in terms of y), as well as parametric form (i.e. y in terms of a parameter e.g. p, and x in terms of the same parameter e.g. p)

Curves to Sketch in Cartesian Form

You are expected to use the graphic calculator to sketch these graphs. Click on the link below to see step-by-step tutorial on how to sketch these graphs using the graphic calculator.

Sketching curves written in parametric form

A parametric equation is one in which a few quantities are expressed as a function of a parameter.

This is an example of a parametric equation:

y = cos t; x= sin t

In this article here, I explain step-by-step how to sketch parametric equations using the graphic calculator.

Transformation of graphs

In this chapter, we learn how to transform (scale, translate, reflect, etc.) these graphs from y = f(x):

Read here where I explain how to do each type of transformation.

The H2 A Level exam often tests students on multiple transformations. Learn how to do multiple transformations, and the recommended order here.

Functions

In the function chapter, students learn what functions are and then apply them to :

  • finding the range / domain of functions
  • what is one-one function
  • inverse functions
    • condition for them to exist (i.e. they have to be one-one)
    • finding range/ domain of inverse functions
    • finding the rule of an inverse function
  • composite functions
    • condition for composite functions to exist
    • finding range/ domain of composite functions
    • finding the rule of a composite function

You’ll find the detailed notes on this chapter on functions here.

Vectors

In H2 Math, vectors is a (very) long chapter. I’ll recommend looking at points below, and testing yourself what’s the concept behind them, and then click on the link below, to bring you to a detailed explanation on each vector concept in your H2 A Level Math:

Differentiation Techniques

Properties of differentiation

In differentiation techniques, you should be familiar with the different differentiation techniques:

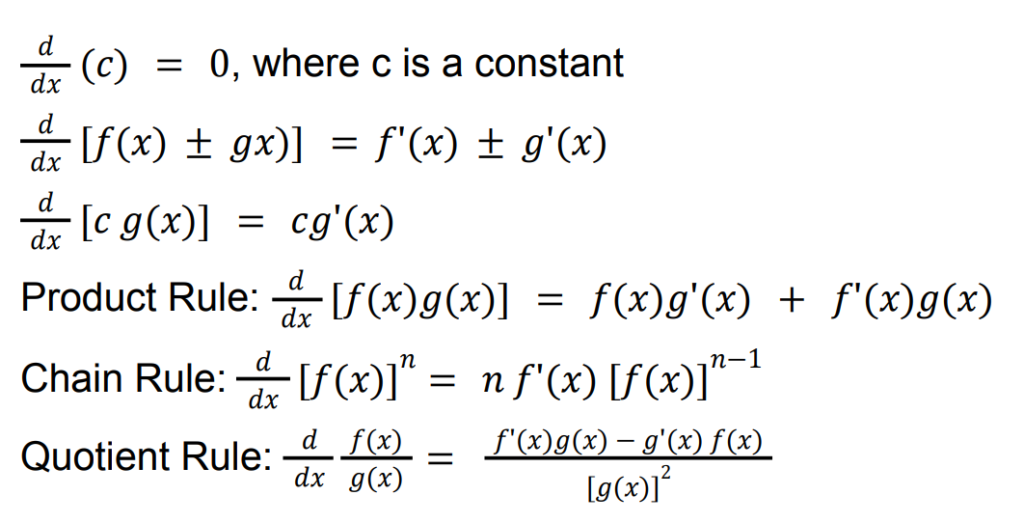
Differentiation Formulae tested in H2 A Level Math

Once you are familiar with those properties of differentiation, and applying chain rule, product rule, quotient rule and so on, it’s time to be familiar with the differentiation formulae that you learn:

Differentiation of Algebraic Functions

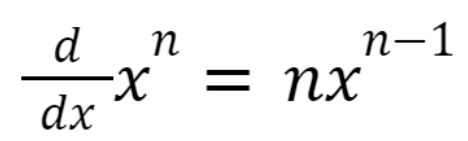
Differentiation of Trigonometric Functions

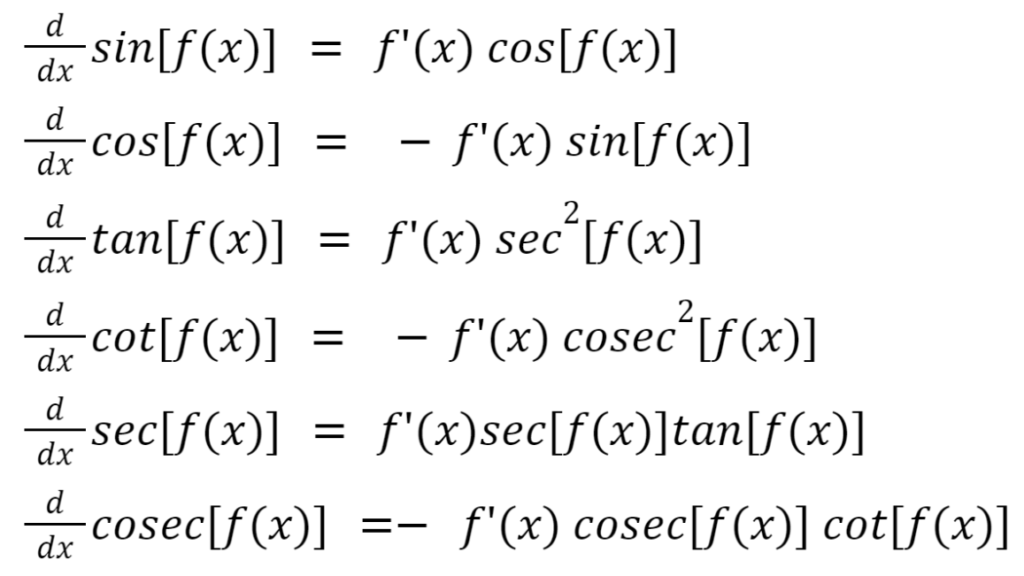
Differentiation of Inverse Trigonometric Functions

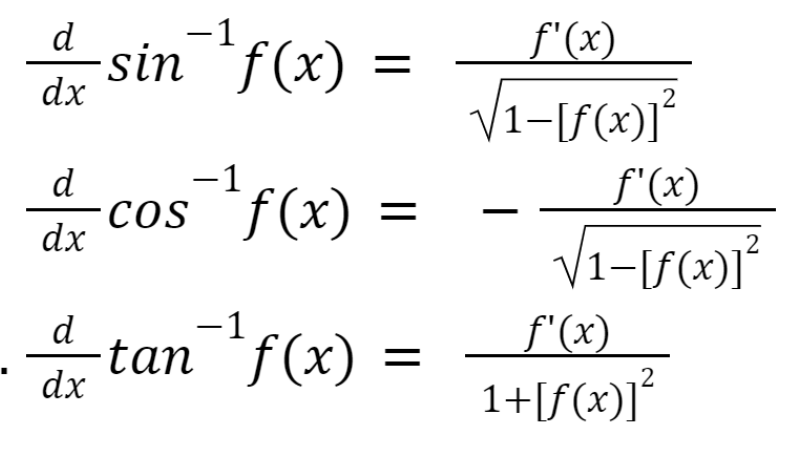
Differentiation of exponential functions

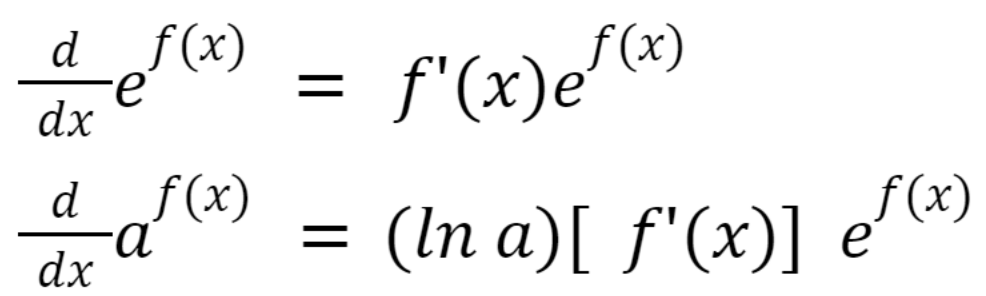
Differentiation of logarithmic functions

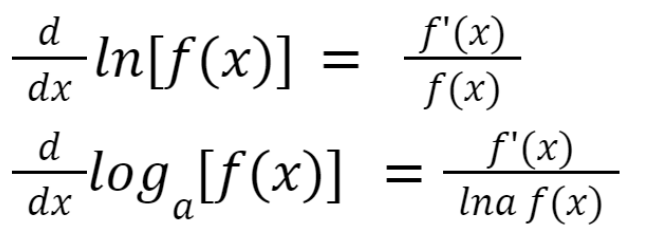
Differentiation of parametric equations

A parametric equation is one in which a few quantities are expressed as a function of a parameter.

This is an example of a parametric equation:

y = cos t; x= sin t

To differentiate a parametric equation, you’ll need to find dy/dt and dx/dt. dy/dx = (dy/dt) /(dx/dt)

Implicit Differentiation

Implicit differentiation is used when we do not have an equation expressed as y in terms of x. When that happens, we use implicit differentiation.

The following is an example of obtaining dy/dx by implicit differentiation:

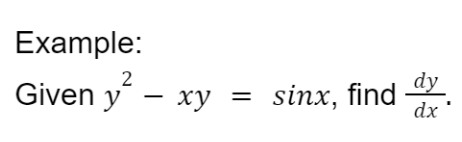
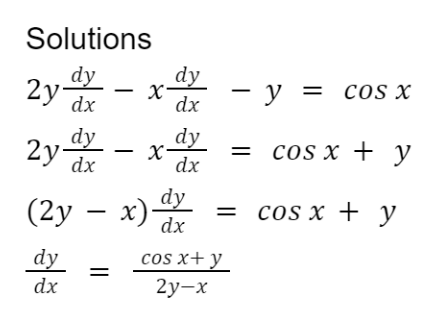
Application of Differentiation

Application of differentiation is a chapter that is very like your A Level Additional Math, just with more added complexity, and with the new formulae you learn at A levels.

In this topic, you learn be tested on:

  • increasing and decreasing functions
  • finding maximum and minimum point
  • application of differentiation to tangents and normals
  • application of differentiation to maximum and minimum problems
  • application of differentiation to rate of change (using chain rule)

I explain in the details the above concepts here.

Integration

Integration at A Level is a huge step from O Level integration. Suddenly, you have way more different ways you can integrate, and you’ll often, it involves trigonometric manipulation (example: 2023 H2 A Level Paper 1 Question 4 integration question ).

In this topic on integration, you’ll need to be familiar with the properties of integration, and all the formulae. I’ve summarized all of them here. Then you’ll need to use your observing eyes to determine which method to use. This comes from experience — i.e. conscious pratice.

Application of Integration

In this section, you’ll apply integration to finding:

Maclaurin’s Expansion

Maclaurin’s expansion can be used to approximate a function, f(x) into a polynomial form. The approximation can be done using this formula here:

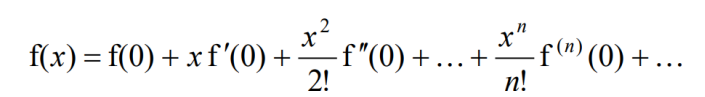
Formula for Maclaurin's Expansion. This formula is also found in the MF26, formula booklet for H2 Math. You do not need to memorize it.

This formula is given in the formula booklet during your A Level Exam, and does not need to be memorized.

Differential Equations

In H2 A Level Math, you are given an equation with dy/dx, y and x, and asked to find y. This is known as a first-order differential equation, and you are to find an expression for y in terms of x using the variable separable method.

Below is an example of solving a differential equation:

a differential equation question for H2 A Level Math
an example question on differential equation

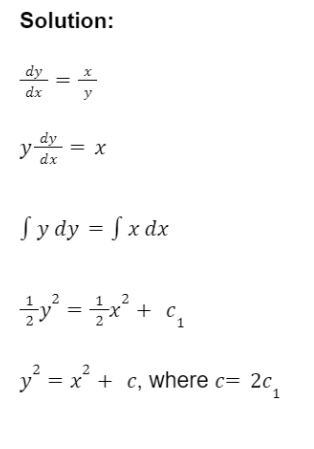
Sequences and Series + Summation Notation

I’ve broken down this chapter on sequences and series into many different parts. Click on the link to learn about each concept:

Arithmetic Progression and Geometric Progression (AP&GP)

Arithmetic Progression

An arithmetic progression is one in which each consecutive term differs by a common difference, d.

If the first term of an arithmetic progression is a, and the common difference is d, then

  • nth term = a + (n-1)d
  • sum of first n terms = 1/2 n[2a+(n-1)d] = 1/2 n [a + nth term]

Geometric Progression (GP)

A geometric progression is one in the ratio of 2 consecutive terms is a constant, r.

r = (nth term)/ ((n+1)th term)

If the first term of a geometric progression is a, and the common ratio is r, then

nth term of the geometric progression = arⁿ⁻¹

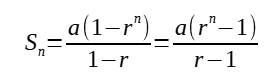
sum of first n terms of a geometric progression

For a geometric progression (GP), the sum to infinity exists or the GP is convergent if |r| <1. If that happens, the sum to infinity can be found be the formula:

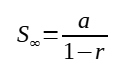
sum to infinity of a geometric series

Hope this crash course on JC1 H2 A Level Math is useful to you! =)

All the notes for H2 A Level Math

Go here to find all the notes and resources for H2 A level Math.

error: Content is protected !!