The equation of ellipses take the form:
(x-H)²/A²- (y-K)²/B² = 1 OR (y-K)²/B² – (x-H)²/A² = 1
Using the Graphic Calculator to obtain a sketch of the ellipse:
Here’s how you can use the Graphic Calculator (Ti-84) to obtain the equation of the hyperbolas:
Step 1: Press [Apps]

Step 2: Select conics

Step 3: Select hyperbolas
Step 4: Select the form of the equation that you have (either option 1 or 2)
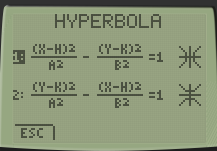
Step 5: Type in the parameters
i.e. H, K , A, B.
Step 6: Press [Graph]
Asymptotes of Hyperbolas
While the Ti 84 graphic calculator is able to give the shape, and maximum and minimum points of the graph, it is unable to give the asymptotes.
The hyperbolas has 2 asymptotes. This can be found finding the limits of the function as x or y tends to ±∞.
For (x-H)²/A²- (y-K)²/B² = 1, we can rewrite it as (x-H)²/A² = 1 +(y-K)²/B².
As x→±∞ , (x-H)²/A² →∞.
This means that on the other side of the equation, 1 +(y-K)²/B² →∞. 1 is insignificant, compared to ∞. 1 +(y-K)²/B²≈ (y-K)²/B². This means that as x→±∞, (x-H)²/A²≈(y-K)²/B². Hence, as x→±∞, ±(x-H)/A = (y-K)/B or y =±B(x-H)/A + K.
Hence, the hyperbola (x-H)²/A²- (y-K)²/B² = 1 has the asymptotes y =±B(x-H)/A + K.
Using the same method, you’ll notice that the asymptote for (y-K)²/B² – (x-H)²/A² = 1 is similar to that of (x-H)²/A²- (y-K)²/B² = 1.
