In this post, let’s look at how to solve inequalities involving polynomial.
Let’s start off by looking at the steps needed to solve the polynomial inequalities:
Step 1: Determine the values that x cannot take (because denominator cannot be 0).
Step 2: Put all the non- zero terms on one side of the inequality, and make the other side of the inequality 0
Step 3: Combine everything on the non-zero side into a single fraction.
Step 4: Completely factorize the numerator and denominator.
Step 5: Determine the values that make numerator 0 or denominator 0.
Step 6: Put the numbers from step 5 into the number line. Put an open circle around the numbers that x cannot take (from step 1).
Step 7: Determine whether the polynomial fraction is positive or negative for each of the range.
Step 8: Determine the solution (remember to exclude values from step 1).
Example: Solve the following inequality involving polynomial fractions:
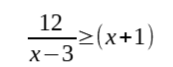
Step 1: Determine the values that x cannot take (because denominator cannot be 0).
Since we only have 1 denominator here, x-3, it cannot be 0. Hence, x≠ 3.

Step 2: Put all the non- zero terms on one side of the inequality, and make the other side of the inequality 0.
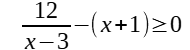
Step 3: Combine everything on the non-zero side into a single fraction.
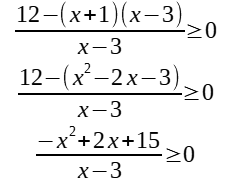
Step 4: Completely factorize the numerator and denominator.
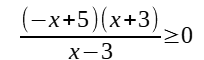
Step 5: Determine the values that make numerator 0 or denominator 0.
Values that make numerator 0 are 5 and -3.
Values that make denominator 0 is 3.
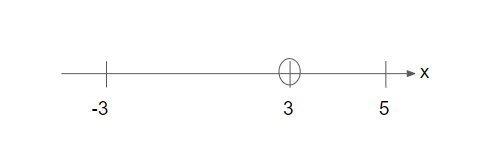
Step 6: Put the numbers from step 5 into the number line. Put an open circle around the numbers that x cannot take (from step 1).
From step 5 we obtained these values of x: 5, -3 and 3.
We’ll put these numbers on the number line.
In addition, from step 1, x ≠ 3. Hence, we’ll put an open circle around 3 to remember that x cannot take this value.
Step 7: Determine whether the polynomial fraction is positive or negative for each of the intervals.
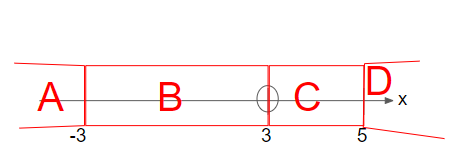
For interval A, where x is lesser than -3, we’ll substitute a value lesser than -3 into (-x+5)(x+3)/(x-3). For instance, we’ll substitute x=-4 in. (-(-4)+5)(-4+3)/(-4-3) = 9/7 > 0
Hence, we’ll put in a positive sign in A.
For interval B, where x is between -3 and 3, we can substitute any value within this range into (-x+5)(x+3)/(x-3). For instance, we’ll substitute x = 0 in. (-0+5)(0+3)/(0-3)= -5 < 0.
Hence, we’ll put in a negative sign in B.
For interval C, where x is between 3 and 5, we can substitute any value within this range into (-x+5)(x+3)/(x-3). For instance, we’ll substitute x = 4 in. (-4+5)(4+3)/(4-3)= 7 > 0.
Hence, we’ll put in a positive sign in C.
For interval D, where x is more than 5, we’ll substitute a value more than 5 into (-x+5)(x+3)/(x-3). For instance, we’ll substitute x=6 in. (-(6)+5)(6+3)/(6-3) = -3 < 0
Hence, we’ll put in a negative sign in D.
The number line now looks like this:
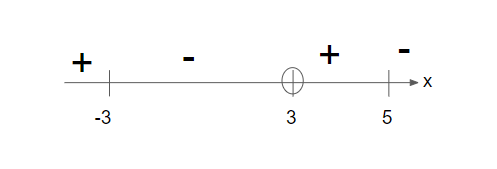
Step 8: Determine the solution (remember to exclude values from step 1).
Since we are interested in (-x+5)(x+3)/(x-3) ≥ 0, we are interested in the positive portion of (-x+5)(x+3)/(x-3) and the portions that gives (-x+5)(x+3)/(x-3) a value of 0.

From the number line, the solution for 12/(x-3)≥ x+1 is x≤-3 or 3<x≤5.
Learn H2 A Level Math Inequalities
Here are the complete notes for solving inequalities for H2 Math:
- Solving inequalities using the graphic calculator
- Solving inequalities involving polynomials
- Solving inequalities involving polynomial fractions
- Quadratic functions that are always positive or negative
- Solving inequalities with functions that are always positive or negative
- Modulus Functions
- Solving inequalities involving modulus functions 1
- Solving inequalities involving modulus functions 2
- Solving inequalities involving modulus functions 3
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
