A vector has both direction and magnitude.
Equal vectors
2 vectors are equal to each other when they have the same direction and same magnitude. 2 vectors are said to be equal if:
- they are parallel and point in the same direction AND
- they have the same magnitude (or length)
Addition of vectors
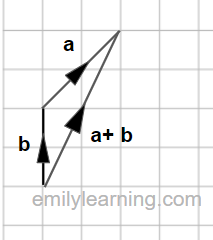
When we add vectors we find the resultant magnitude and direction. 2 vectors can be added using the triangle rule. To do add 2 vectors using the triangle method:
- we need to arrange the vectors such that they “continue” from one another.
- next join the “start” and “end” together
- this will give us the sum of the 2 vectors.
For instance, given the vectors a and b as shown below, draw a vector to represent a+b.
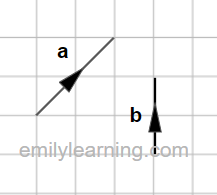
Adding vector a to b by triangle rule gives a+b:
Negative vectors
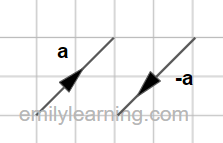
When we put a negative sign in front of a vector, we reverse its direction.
For instance, in the diagram below, the difference between a and –a is the direction of the arrow.
Multiplying a vector by a constant
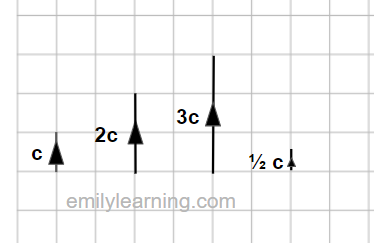
Multiplying a vector by a positive constant, k, will change its magnitude to k times its original, without changing its direction.
The diagram below shows the vectors c, 2c, 3c and ½ c. All these vectors are all parallel to one another. The magnitude (length) of 2c is twice that of c, the magnitude (length) of 3c is thrice that of c, and the magnitude (length) of ½c is half that of c.
Multiplying a vector by a negative constant, -k, will reverse the direction of the constant, and its magnitude becomes k times its original.
The diagram below shows that vectors c and -2c. Observe that these 2 vectors are:
- parallel to each other
- direction of -2c is the reverse of that of c
- magnitude of -2c is twice that of c

Notes on H2 Math Vectors
You’ll find all the notes on H2 A Level Math Vectors topic here.
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
