Application of Differentiation for H2 A Level Math

In application of differentiation for H2 A Level Math, you’ll apply differentiation to:

Increasing and Decreasing Functions

For a graph of y = f(x), it is said to be increasing when f'(x) > 0, and decreasing when f'(x) < 0.

The gradient of a tangent to the curve at x = dy/dx

The gradient of a normal to the curve at x = – 1/ (dy/dx)

Rate of change questions often involve the use of chain rule to connect related rates of change (e.g. connect rate of change of y to x).

For example, the rate of change of y and x can be connected using the chain rule:

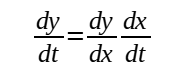
Stationary points occur when dy/dx = 0.

We’ll look at 2 types of stationary points in detail: maximum point and minimum point

At maximum point, dy/dx = 0, d²y/dx² < 0.

At minimum point, dy/dx = 0, d²y/dx² > 0.

When doing a question involving maximum and minimum, you can make use of differentiation.

If we have an equation involving A and A is written in terms of x e.g. A = f(x), to find maximum or minimum do the following:

Find f'(x)
Let f'(x) = 0 and find x.
To determine if the x value from the above step gives maximum or minimum A, find f”(x). if f”(x) < 0 then A is a maximum, if f”(x) > 0, then A is a minimum.

Apart from using the second derivative test to determine maximum or minimum, we can also use a table method.

x	x- (value slightly smaller than x)	x	x+ (value slightly larger than x)
dy/dx	<0	0	>0
Shape	\	_	/
	minimum point

x	x- (value slightly smaller than x)	x	x+ (value slightly larger than x)
dy/dx	>0	0	<0
Shape	/	_	\
	maximum point