A system of linear equations consist of 2 or more linear equations. Linear equations are equations where the unknown variable has a power of 1.
The following is an example of a system of linear equation:
x+y = 0
2x- y = 3
Notice that in the above example, there are 2 variables, x and y. Since both x and y have a power of 1 of in the equations, these are linear equations. When we have 2 unknowns, we’ll need at least 2 equations to obtain a solution for the 2 unknowns.
In general, if there are n unknowns, at least n equations are needed to obtain a solution for them.
Solving system of linear equations using the graphic calculator Ti84
Let’s look at how to solve a system of linear equations using the example:
Solve for x, y and z given x+ y+ z = 2, x-z+ 2y +1 = 0, 2x +2y +3z = 3.
Step 1: Arrange the equations in the form a₁x₁+b₂x₂ +… = a₀
This means that we’ll need to arrange the equations such that we have variables on the left hand side, and the constant term (i.e. the one that has no constant) on the right hand side of the equal sign.
Also, we should arrange the equations such that on the left hand side, the variable that that comes first , second, third, etc. for each equation is always the same.
Example of how to arrange the system of linear equations:
Let me illustrate this with the example of this system of linear equations: x+ y+ z = 2, x-z+ 2y +1 = 0, 2x +2y +3z = 3
Let’s assume that we want the variables on the left hand side of the equation to be arranged starting with x, then y then z. Hence, all the 3 equations should be written in the form of a₁x+a₂y +a₃z = a₀, where a₁ is the coefficient of x, a₂ is the coefficient of y, and a₃ is the coefficient of z.
Doing this for all the 3 equations in the system of linear equations gives:
x+ y+ z = 2
x+ 2y -z = -1
2x +2y +3z = 3
Step 2: Press [Apps] on your GC

Step 3: Select Polysmlt2
Note: if Polysmlt2 is not available in your graphic calculator Ti84, you can download it from the Texas Instrument website here.
Step 4: Select SIMULT EQN SOLVER
Step 5: Set the number of equations and number of unknowns.
You can leave the other options unchanged. Only exception is when you are dealing with trigonometry, you may like to select the correct mode e.g. degrees of radians.
For this example of system of linear equation, we have 3 unknowns (x , y and z), and 3 equations:
x+ y+ z = 2
x+ 2y -z = -1
2x +2y +3z = 3
Hence, we’ll select the option of 3 unknowns and 3 equations.
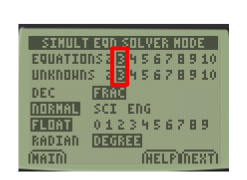
Once done, press the button that is right beneath [next] in the screen. This button is [graph]
Step 6: Type in the coefficients and constant terms according to the equation.
For x+ y+ z = 2, we’ll type it as 1 1 1 | 2.
For x+ 2y -z = -1, we’ll type it as 1 2 -1|-1
2x +2y +3z = 3, we’ll type it as 2 2 3| 3

Once we have typed in all the values, press the button directly beneath [solve], i.e. [graph].
Step 7: Obtain the solutions
We’ll obtain the following:
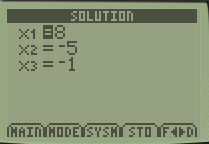
x1 corresponds to the x in our example, x2 corresponds to y in our example, and x3 corresponds to z in our example.
Hence, x = 8, y = -5 and z = -1.
