In this lesson, we’ll look at how to find the equation of a plane in cartesian and vector form.
Equation of plane in vector form
To find the equation of a plane in vector form, you’ll first need to find a vector normal (i.e. perpendicular) to the plane. We call this vector normal to the plane the normal vector, n, of the plane.
Once n is found, we’ll still need a position vector of a point that lies on the plane. Assuming that a is the position vector of a point that lies on the plane, then the vector equation of the plane is: r . n = d, where d= a.n.
Equation of plane in cartesian form
The cartesian equation of a plane takes the form ax + by + c = d, where a, b, c and d are constants to be determined.
Convert the equation of a plane from vector form to cartesian form
To convert a plane equation from vector form to cartesian form involves rewriting it from r . n = d to ax + by + c = d.
To do so, we’ll rewrite r as:
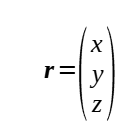
Then do a dot product between r and n.
These will convert the vector equation of the plane to a cartesian equation.

Convert the equation of a plane from cartesian form to vector form
To convert a plane equation from vector form to cartesian form involves rewriting it from ax + by + c = d to r . n = d.
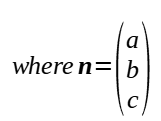
Example:
Given the equation of the plane is 2x – 3y -z = 4, find (i) a vector normal to the plane (ii) find the vector equation of the plane.

Notes on H2 Math Vectors
You’ll find all the notes on H2 A Level Math Vectors topic here.
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
