In this post, let’s look at how to solve inequalities involving polynomial.
Let’s start off by looking at the steps needed to solve the polynomial inequalities:
Step 1: Put all the non- zero terms on one side of the inequality, and make the other side of the inequality 0
Step 2: Completely factorize the side with the polynomial
Step 3: Determine the values that will make the polynomial 0.
Step 4: Put the values in step 3 on a number line.
Step 5: Determine whether the polynomial is positive or negative at the intervals on the number line.
Step 6: Determine the solution.
Example 1: Solve the inequality (x-3)(x+2)(x-1)>(x-3)(x+1)
Step 1: Put all the terms to one side, and make the other side 0.
(x-3)(x+2)(x-1)-(x-3)(x+1)>0
Step 2: Completely factorize the side with the polynomial
(x-3)(x-1)[(x+2)-(x+1)]>0
(x-3)(x²-3) > 0
(x-3)(x+√3)(x-√3)>0
Step 3: Determine the values that will make the polynomial 0.
For the polynomial (x-3)(x+√3)(x-√3), it is equal to 0 when x = 3, -√3 or √3
Step 4: Put the values in step 3 on a number line.

Step 5: Determine whether the polynomial is positive or negative at the intervals on the number line.
I’ve marked out the 4 intervals that we are interested in, and labelled them A, B, C and D.
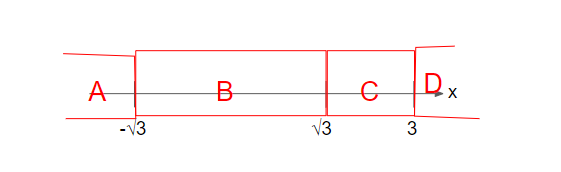
Let’s look at interval A. Interval A consists of x values that are lesser than -√3.
Let’s put any value of x lesser than -√3 into (x-3)(x+√3)(x-√3). E.g., let’s substitute x = -4 into it. (-4-3)(-4+√3)(-4-√3) =-91 < 0
Hence, we’ll put a negative sign at A.
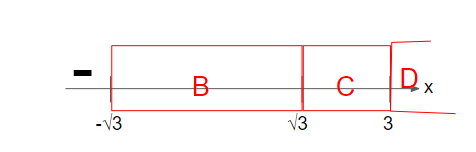
Next, let’s look at interval B. Interval B consists of x values between -√3 and √3.
Let’s put any value of x between -√3 and √3 into (x-3)(x+√3)(x-√3). E.g., let’s substitute x = 0 into it. (0-3)(0+√3)(0-√3) =9 > 0.
Hence, we’ll put a positive sign at B.
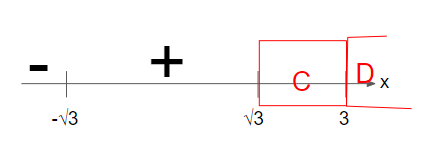
Next, let’s look at interval C. Interval C consists of x values between √3 and 3.
Let’s put any value of x between √3 and 3 into (x-3)(x+√3)(x-√3). E.g., let’s substitute x = 2 into it. (2-3)(2+√3)(2-√3) =-1 < 0.
Hence, we’ll put a negative sign at C.
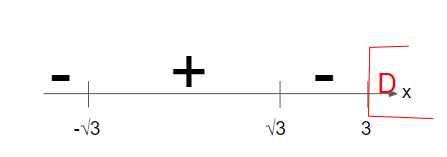
Finally, let’s look at interval D. Interval D consists of x values more than 3.
Let’s put any value of x more than 3 into (x-3)(x+√3)(x-√3). E.g., let’s substitute x = 4 into it. (4-3)(4+√3)(4-√3) =13 > 0.
Hence, we’ll put a positive sign at D.
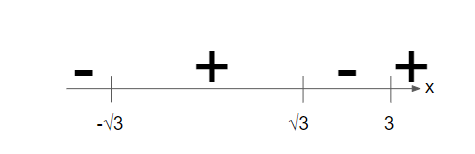
Step 6: Determine the solution.
Since we are solving for (x-3)(x+√3)(x-√3)>0, we are interested in the range of values of x that makes (x-3)(x+√3)(x-√3) positive. From the number line obtained from step 5, we know that this occurs when -√3<x<√3 or x > 3 (see the region highlighted in yellow below).
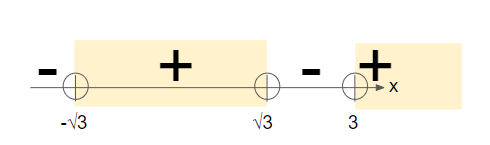
Hence, the solution to (x-3)(x+2)(x-1)>(x-3)(x+1) is -√3<x<√3 or x > 3.
Learn H2 A Level Math Inequalities
Here are the complete notes for solving inequalities for H2 Math:
- Solving inequalities using the graphic calculator
- Solving inequalities involving polynomials
- Solving inequalities involving polynomial fractions
- Quadratic functions that are always positive or negative
- Solving inequalities with functions that are always positive or negative
- Modulus Functions
- Solving inequalities involving modulus functions 1
- Solving inequalities involving modulus functions 2
- Solving inequalities involving modulus functions 3
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
