In this post, we’ll look at the following transformation of y = f(x) into :
Transformation of y = f(x) into y = af(x)
Transformation of y= f(x) into y= af(x) involves scaling y= f(x) by a units parallel to the y- axis.
Example question on transformation question involving scaling parallel to y-axis
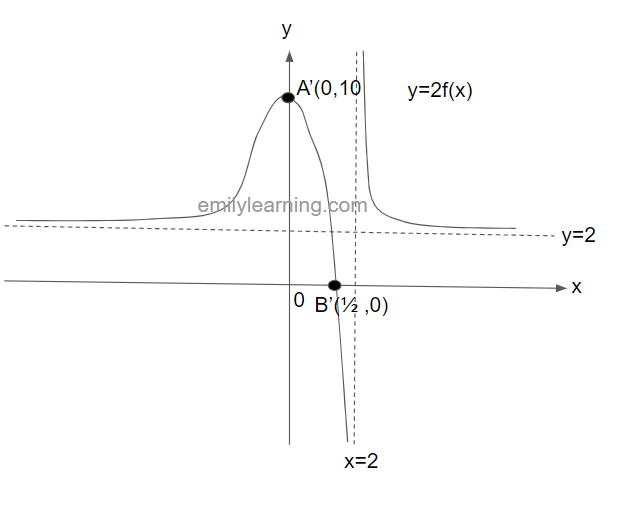
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = 2f(x).

Solution:
To sketch y = 2f(x), we will scale the graph of y = f(x) by a scale factor of 2 parallel to the y-axis. This will give us the following graph:
Transformation of y = f(x) into y = f(ax)
Transformation of y = f(x) into y = f(ax) involves scaling y = f(x) by 1/a units parallel to the x-axis.
Example question on transformation question involving scaling parallel to x-axis
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = f(2x).

Solution:
To sketch y = f(2x), we will scale the graph of y = f(x) by a scale factor of 1/2 parallel to the x-axis. This will give us the following graph:

Transformation of y = f(x) into y = f(x) + a
Transformation of y = f(x) into y = f(x) +a involves a translation of y = f(x) by a units in the y direction.
Example question on transformation question involving translation in the y- direction
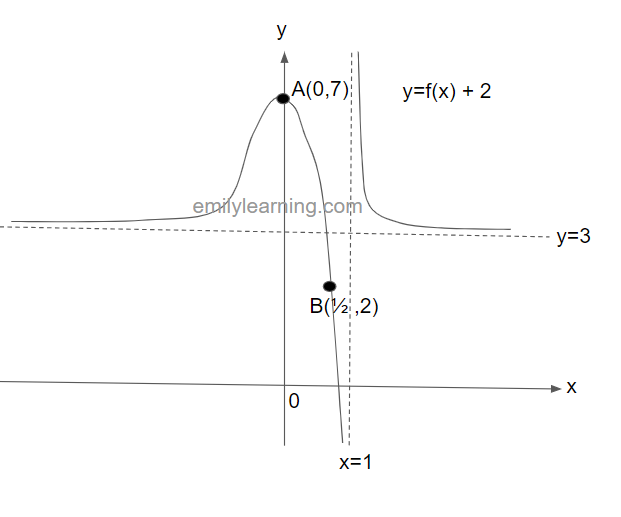
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = f(x)+ 2.

Solution:
To sketch y = f(x)+2, we will translate the graph of y = f(x) by a scale factor of 2 in the y-direction. This will give us the following graph:
Transformation of y = f(x) into y = f(x+a)
Transformation of y = f(x) into y = f(x+a) involves a translation of y = f(x) by -a units in the x direction.
Example question on transformation question involving translation in the x- direction
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = f(x+2).

Solution:
To sketch y = f(x+2), we will translate the graph of y = f(x) by a scale factor of 2 in the x-direction. This will give us the following graph:

Transformation of y = f(x) into y = f(-x)
Transformation of y = f(x) into y = f(-x) involves reflecting the graph of y= f(x) about the x- axis.
Example question on transformation question involving reflection about the x- axis
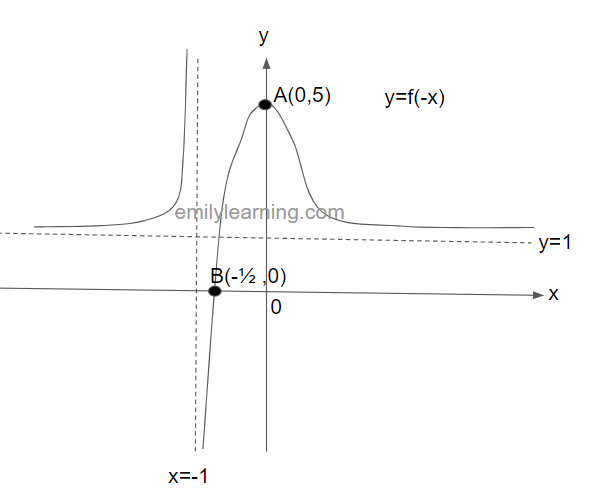
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = f(-x).

Solution:
To sketch y = f(-x), we will reflect the graph of y = f(x) about the x-axis. This will give us the following graph:
Transformation of y = f(x) into y = -f(x)
Transformation of y = f(x) into y = -f(x) involves reflecting the graph of y= f(x) about the y- axis.
Example question on transformation question involving reflection about the y- axis
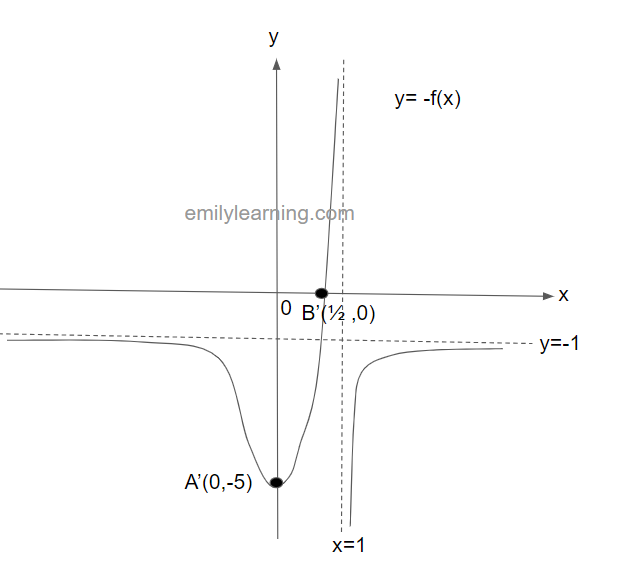
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = -f(x).

Solution:
To sketch y = f(-x), we will reflect the graph of y = f(x) about the y-axis. This will give us the following graph:
Transformation of y = f(x) into y = |f(x)|
Transformation of y= f(x) into y = |f(x)| involves reflecting the part of y= f(x) below the x-axis about the y-axis.
Example question on transformation of y=|f(x)| from y = f(x)
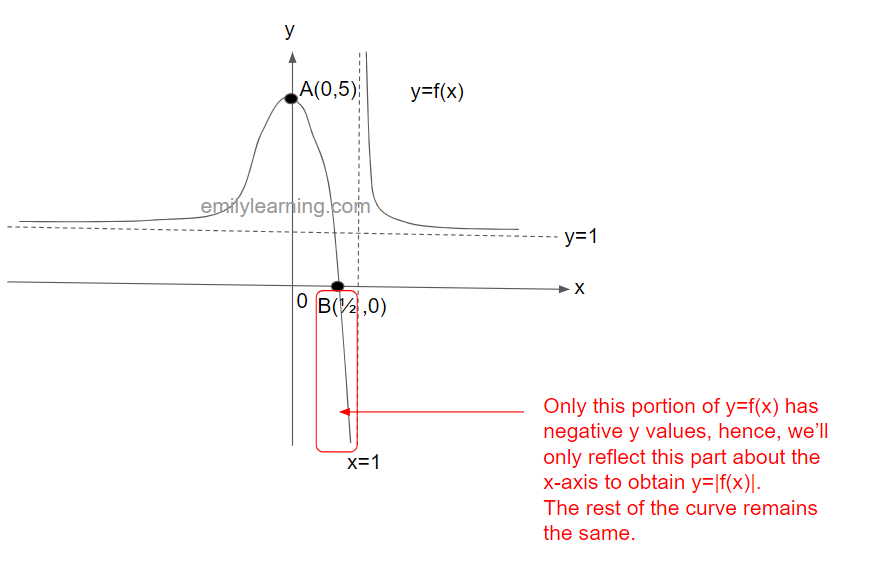
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = |f(x)|.

Solution:
To sketch y= |f(x)| from y = f(x), we’ll only reflect the part with negative y- values about the x-axis. The rest of the curve remains unchanged.
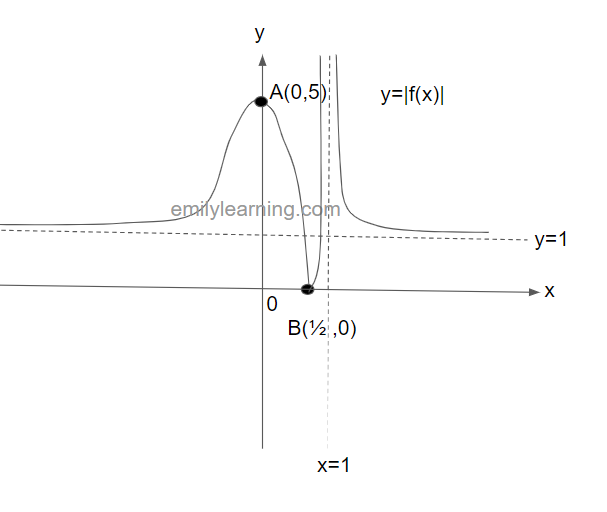
Hence, the graph of y = |f(x)| looks like this:
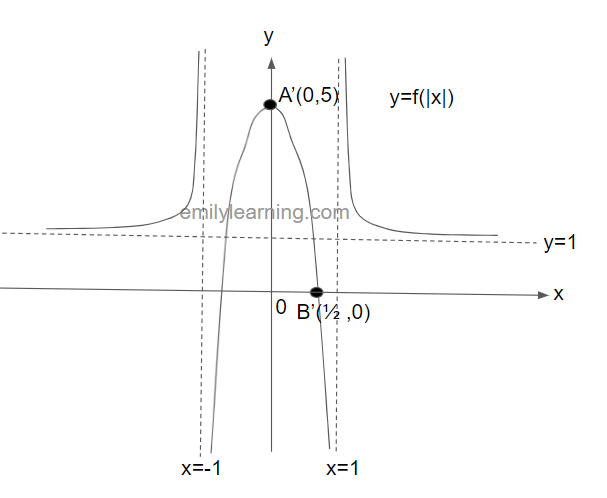
Transformation of y = f(x) into y = f(|x|)
Transformation of y= f(x) into y =f(|x|) involves keeping the part on the positive x-axis, and then reflecting that about the y-axis.
You can do this in 3 steps:
Step 1: Keep the portion of y = f(x) with positive x values.
Step 2: “Erase” the portion of y= f(x) with negative x values
Step 3: Reflect the portion frrom step 1 about the y-axis.
Example question on transformation of y=f(|x|) from y=f(x)
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = f(|x|).

Solution
To obtain y=f(|x|) from y = f(x), we’ll first keep the part of y=f(x) with positive x-values.

Next, we’ll “erase” the entire portion of y= f(x) with negative x values.
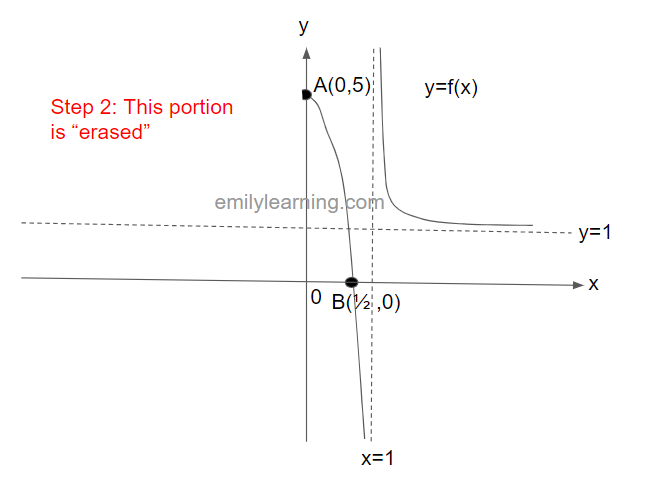
Finally, we’ll reflect the portion on the positive x-values about the y-axis, and we’ll obtain y = f(|x|):
Transformation of y = f(x) into y =1/f(x)
To convert y= f(x) into y=1/f(x), do these:
- all y values of y = f(x) becomes 1/y in y = 1/f(x)
- x-intercepts of y = f(x) becomes vertical asymptotes of y= 1/f(x)
- horizontal asymptotes y = a becomes horizontal asymptotes at y = 1/a. Only exception is asymptotes at y = 0 , where they are no longer asymptotes in the y = 1/f(x) graphs
- maximum point of y = f(x) becomes minimum point of y = 1/f(x); minimum point of y = f(x) becomes maximum point of y = 1/f(x)
- vertical asymptotes at x = a becomes x- intercepts.
Example question on transformation of y=1/f(x) from y=f(x)
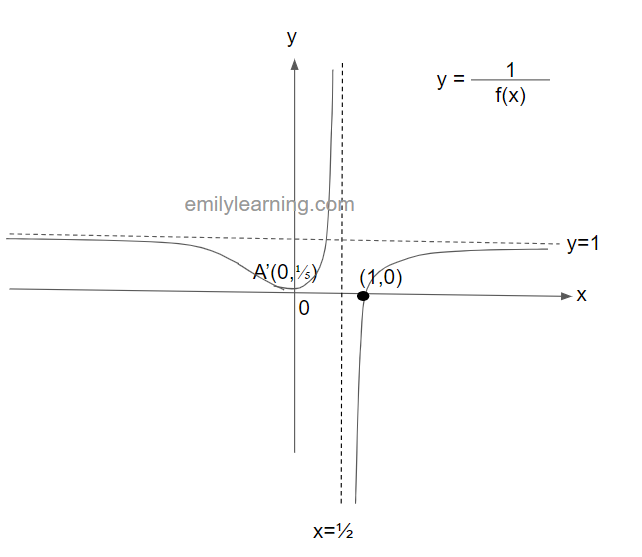
The graph below shows y = f(x). This graph passes through the points A(0,5) and B(1/2, 0), and have asymptotes at x = 1 and y = 1. In a separate diagram, sketch y = 1/f(x).

Solutions
Below shows y=f(x) in black, and the red portions as workings to sketch y = 1/f(x)
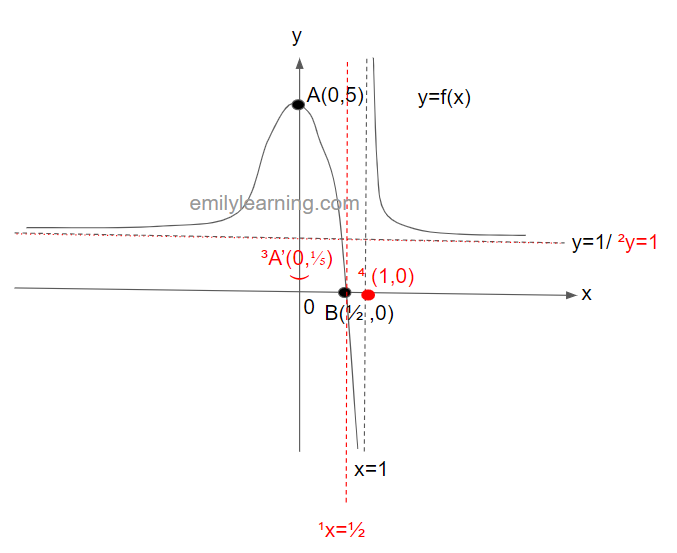
¹x-intercepts of y = f(x) becomes vertical asymptotes of y= 1/f(x) –>hence we now have an x intercept at x= 1/2 for y = 1/f(x)
²horizontal asymptotes y = a becomes horizontal asymptotes at y = 1/a. Only exception is asymptotes at y = 0 , where they are no longer asymptotes in the y = 1/f(x) graphs –> hence, the horizontal asymptote of y = 1/f(x) is y= 1.
³maximum point of y = f(x) becomes minimum point of y = 1/f(x); minimum point of y = f(x) becomes maximum point of y = 1/f(x). –> hence, y = 1/f(x) has a minimum point at (0, 1/5).
⁴vertical asymptotes at x = a becomes x- intercepts. –> hence, y = 1/f(x) has an x-intercept at (1,0).
With these, a sketch of y = 1/f(x) will look be: