Here’s the worked solutions for the 2023 H2 A Level Mathematics Paper 1. Click on the question number to go to the question directly.
Worked solutions for 2023 H2 A Level Mathematics Paper 1
Question 1
This question is on application of differentiation to tangents.
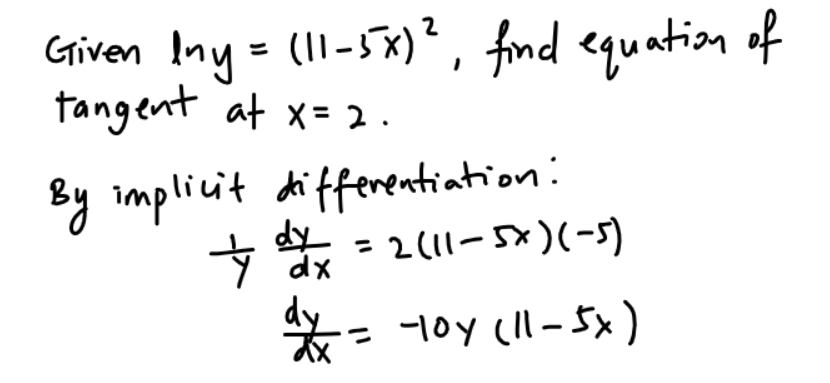
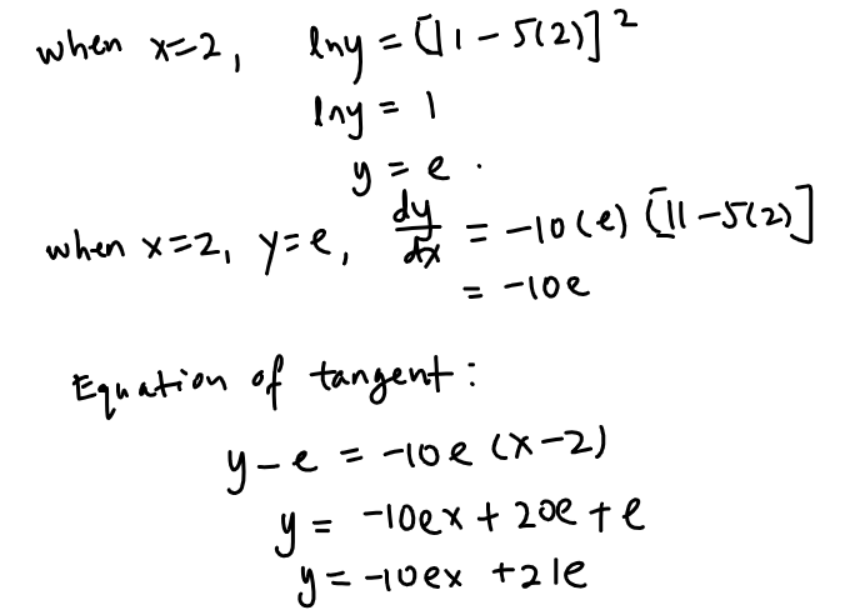
Question 2
This question is on systems of linear equation. As usual, the graphic calculator (G.C) should be used to speed up solving of the question.
(a)

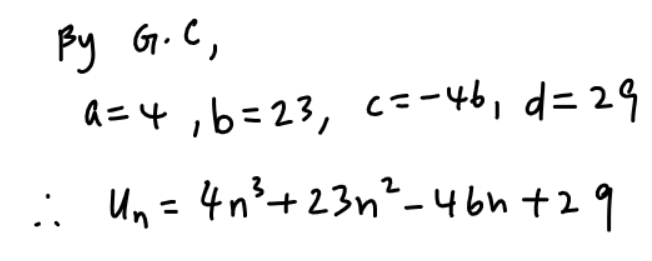
(b)

Question 3
This question is on vectors.
3(a)

3(b)
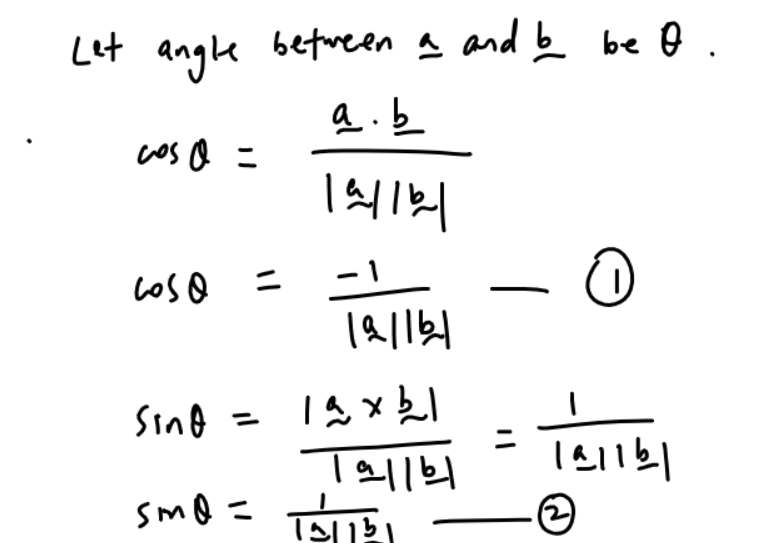
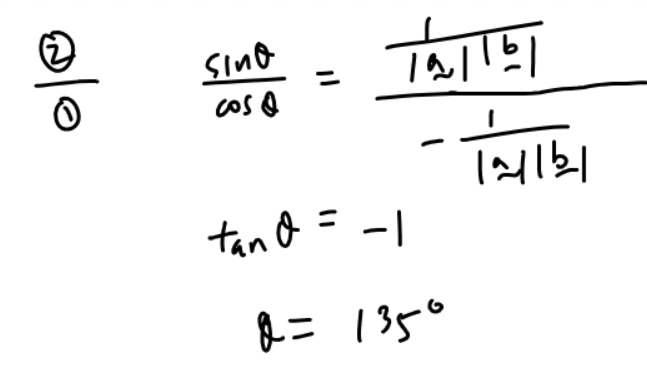
Question 4
This is a question on integration.
(a) In this trigonometric integration, students are expected to use the factor formula which is available in the data booklet:

Worked solutions for question 4a:

(b) This is an integration by parts question. With an algebraic function (x), and a trigonometric function i.e. cos nx, it is an indication that you should be using by parts for integration.

(c)
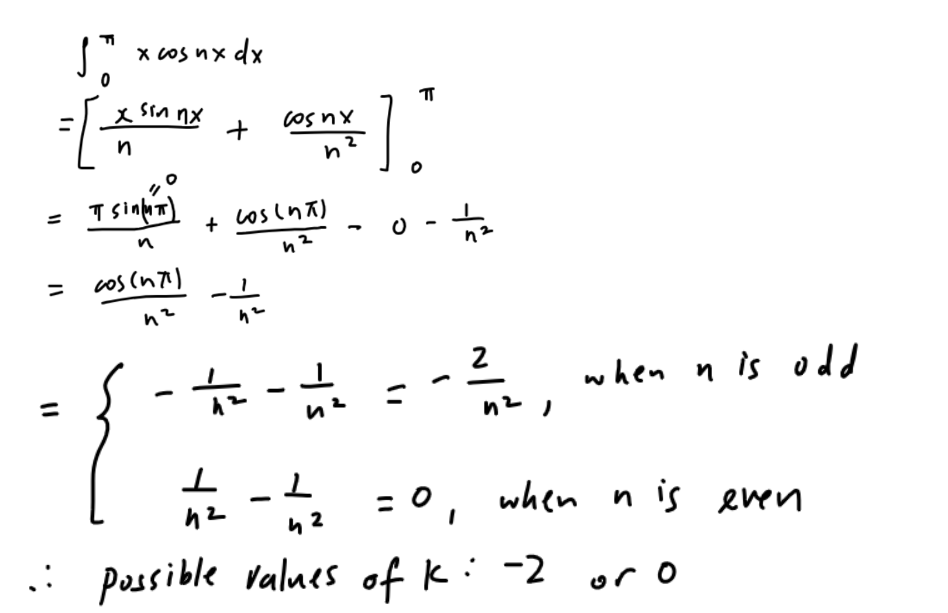
(d)
This question involves integration of modulus function.

Question 5
This is a question on sequences and series.
(a) This question is on method of difference.

(b)

(c)
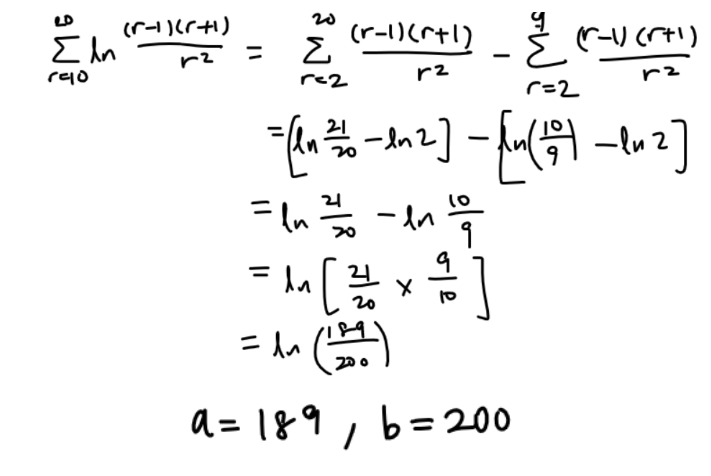
Question 6
(a) This question involves proving of trigonometric identity using the double angle formula. The identity you should use from the data booklet is the one I highlighted below:

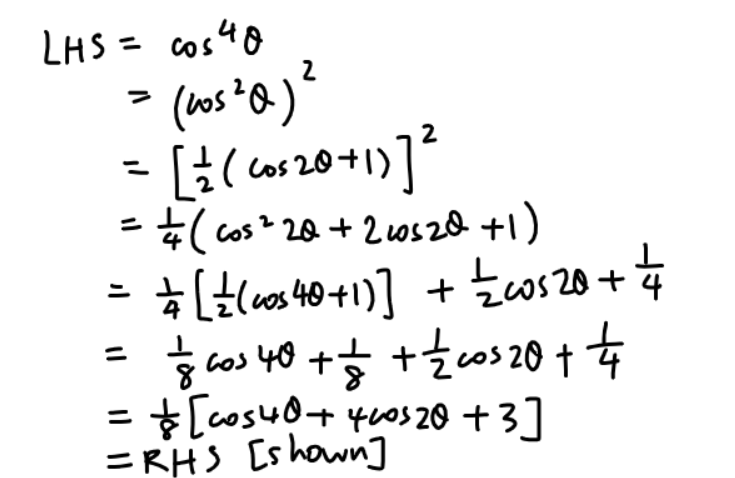
(b)

Hence, volume generated can be found using:

The question specifically talks about finding the exact value of the integral by substitution. In part (a), we have proved a trigonometric identity, that asks us to show that cos⁴θ = 1/8[cos4θ + 4cos2θ + 3]. The left side of this identity cannot be easily integrated, but the right side can. Hence, this is an indication that we need to change what’s to be integrated into something close to cos⁴θ, and then replace cos⁴θ by 1/8[cos4θ + 4cos2θ + 3].
Since y² = (9-x²)^(1.5), and we need something that is close to cos⁴θ, very likely x = 3cos θ

Question 7
(a) This is a question on curve sketching. You can use the G.C to find the x-intercepts, y-intercepts and shape of the graph. Asymptotes have to be deduced.

(b)
Range of f = [0, ∞)
(c)
Range of f = [0, ∞)
Domain of f = (-∞,∞) \ 3
For f² to exist, range of f ⊆ domain of f.
However, [0, ∞) ⊈ (-∞,∞) \ 3
Hence, f² does not exist.
(d)
For f⁻¹ to exist, f has to be a one-one function. From the graph, maximum value of a is -2.
(e)
When domain of f = (-∞, 2]
Range of f = [0, -2) = domain of f⁻¹
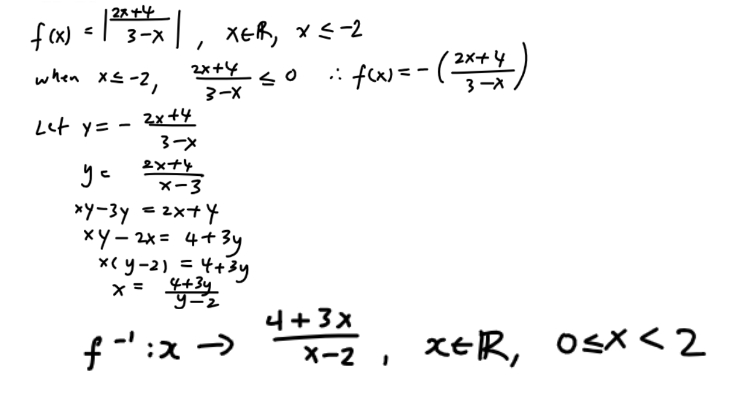
Question 8
This is a complex number question
(a)(i)

(a)(ii)

(b)


Question 9
This question is on vectors.
(a)


(b)(i)


(ii)

(c)

Question 10
This question is on differential equations.
(a)

(b)

(c)

(d)

(e)(i)

(ii)
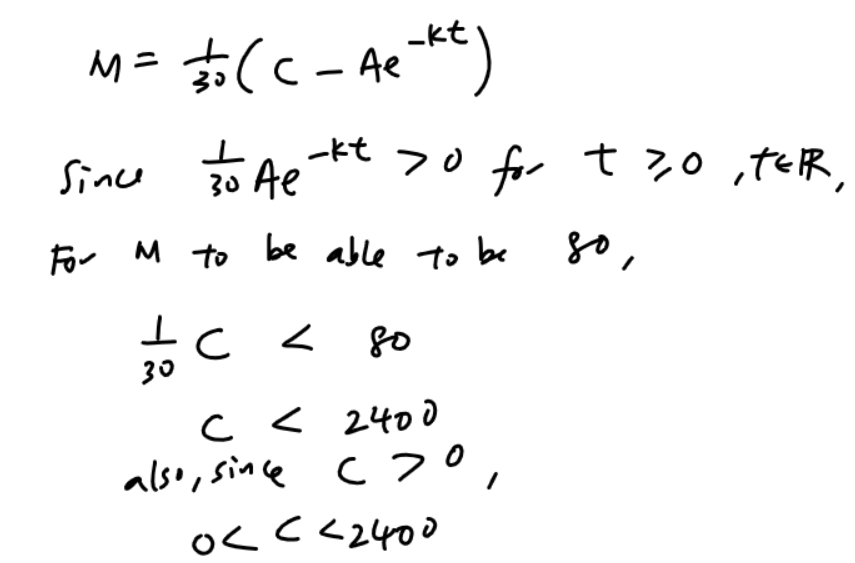
Question 11
This question is on Arithmetic and Geometric Progression (AP & GP)
(a)
| month number | amount deposited ($) | total amount in bank ($) |
| 1 (31 Jan 2021) | a | a |
| 2 (28 Feb 2021) | a+ 50 | a + a+ 50 = 2a + 50 |
| 3 (31 Mar 2021) | a+ 100 | 2a + 50 + a + 100 = 3a + (50 + 100) |
| . . . | . . . | . . . |
| n | a + 50(n-1) | an + [50 + 100 + … + 50(n-1)] |
| . . . | . . . | . . . |
| 36 (31 Dec 2023) | a + 50(35) | 36a + [50 + 100 + … + 50(35)] |
Total amount in bank in 31 Dec 2023 = 36a + [50 + 100 + … + 50(11)] = 36a + 35/2[50 + 35(50)] = $(36a + 31500)
36a + 31500 > 50 000
a > 513.8888
Smallest a = $513.89
(b)
| month | amount owed at beginning of month ($) | amount owed at end of month ($) |
| 1 | 1.001(400,000) | 1.001(400,000) – x |
| 2 | 1.001[1.001(400,000) – x] = 1.001²(400,000) – 1.001x | 1.001²(400,000) – 1.001x – x |
| 3 . . . | 1.001[1.001²(400,000) – 1.001x – x] =1.001³(400,000) – 1.001²x – 1.001x | 1.001³(400,000) – 1.001²x – 1.001x -x . . . |
| n | 1.001ⁿ(400,000) – 1.01ⁿ⁻¹x – 1.01ⁿ⁻²x – … – 1.001x | 1.001ⁿ(400,000) – 1.01ⁿ⁻¹x – 1.01ⁿ⁻²x – … – 1.001x -x |
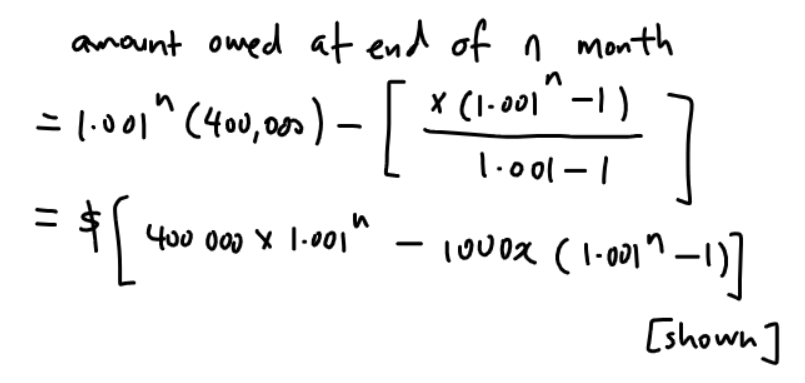
(c)(i)

(c)(ii)

(d)(i)

(d)(ii)
Interest paid in part (d) = 287($1600) + $1320.22 – $400 000 = $60520.22
Interest paid in part (c) = $76506.80
Savings using payment method from (d) = $76506.80 – $60520.22 = $15986.58 = $15990 (3 s.f.)
Watch the step-by-step video explanation for question 11 here: https://youtu.be/iXcDPGFJNM0
For other H2 A Level Math Worked solutions
- Syllabus 9758 Specimen Paper 2025 Paper 2
- Syllabus 9758 Specimen Paper 2025 Paper 1
- Syllabus 9758 Year 2023 Paper 1
- Syllabus 9758 Year 2023 Paper 2
- Syllabus 9758 Year 2022 Paper 1
- Syllabus 9758 Year 2022 Paper 2
- Syllabus 9758 Year 2021 Paper 1
- Syllabus 9758 Year 2021 Paper 2
- Syllabus 9768 Year 2020 Paper 1
- Syllabus 9758 Year 2020 Paper 2
- Syllabus 9758 Year 2019 Paper 1
- Syllabus 9758 Year 2019 Paper 2
- Syllabus 9768 Year 2018 Paper 1
- Syllabus 9758 Year 2018 Paper 2
Learn H2 Math on-demand with our online courses
Find a list of our H2 Math Resources here.
