The equations of circles take the form:
(x-a)²+(y-b)² = r²
where (a, b) is the centre of the circle, and r is the radius.
When the equation of circle is expressed in the form x²+2cx+y²+2dy+e=0, the centre of the circle is (-c, -d) and the radius is √(c²+d²-e).
Using the Graphic Calculator to obtain a sketch of the circle:
Here’s how you can use the Graphic Calculator (Ti-84) to obtain the equation of the curve:
Step 1: Press [Apps]

Step 2: Select conics

Step 3: Select circle

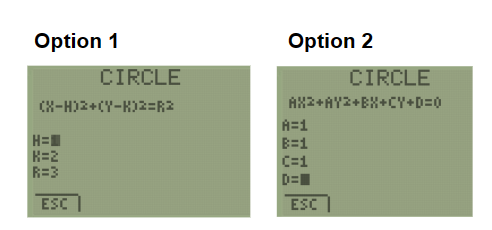
Step 4: Select the form of the equation that you have (either option 1 or 2)
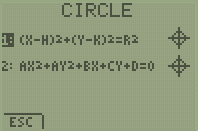
Step 4: Type in the parameters
i.e. H, K and R for option 1; A, B, C and D for option 2.
Step 5: Press [Graph]
Sketching Circles using the graphic calculator
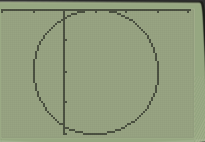
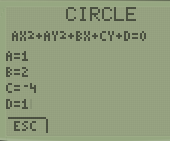
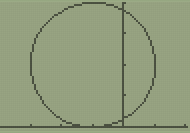
Example 1: Using the graphic calculator, sketch x²+2x+y²-4y+1=0
Worked solutions:
We will use the option 2 form (see step 4) since the equation given is closer to that form:
Sketch given on the GC:
Example 2: Using the graphic calculator, sketch (x-1)²+(y+2)² = 4
Worked Solutions
We will use the option 1 form (see step 4) since the equation given is closer to that form:
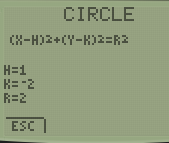
Sketch given on the GC: