In this lesson on vector, we’ll talk about the scalar product of vectors.
How to represent scalar product in Math
We use a ⚫ to represent scalar product, hence, they are sometimes also called dot product.
Definition of scalar product
When we take the scalar product of vector a and b, we are essentially doing this:
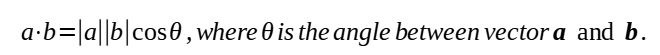
Note that |a||b| cos θ gives a value (numerical value). Hence, the result of a scalar product is a numerical value.
Finding scalar product of vectors expressed in x, y, z- coordinates form
If the vectors are expressed in x, y, z- coordinates form, the scalar product could be found in this manner:
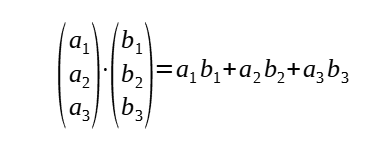
Useful results of scalar product
- Since the same vectors are parallel to each other, and hence angle between them is 0 (i.e. cos0ᵒ = 1) , a . a = |a|²
- Dot product of perpendicular vectors will give 0 (since cos 90ᵒ = 0).
- To find the angle between 2 vectors, we can use the formula cosθ = (a. b )/( |a| |b| )
Notes on H2 Math Vectors
You’ll find all the notes on H2 A Level Math Vectors topic here.
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
