Here’s the worked solutions for the 2023 H2 A Level Mathematics Paper 2. Click on the question number to go to the question directly.
Worked solutions for 2023 H2 A Level Mathematics Paper 2
Section A of 2023 A Level H2 Mathematics (Pure Math)
Question 1
(a)
This question is on solving inequalities. This question is only worth 2 marks, and there is no mention that you cannot use the graphic calculator, hence, this should be solved using the graphic calculator to save time.

(b)
This part is also on solving of inequalities. However, since the question specifically mentions without using the calculator, you’ll have to solve it manually.

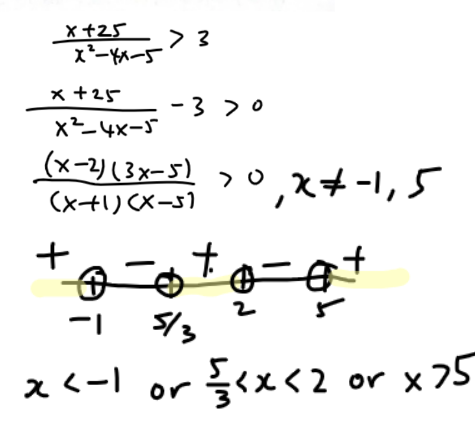
Question 2
This question is on Maclaurin’s series.
(a)
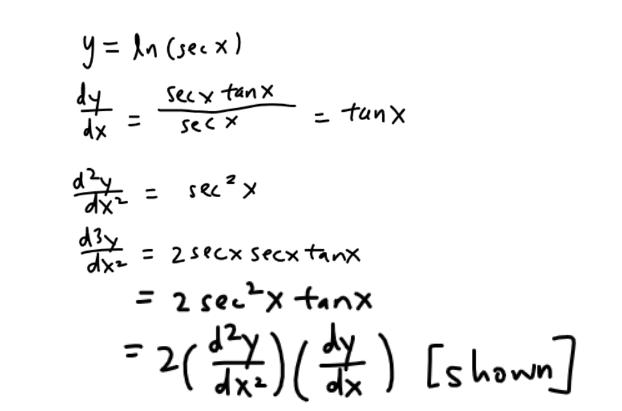
(b)

(c)

(d)

Question 3
This question is on vectors.
3(a)
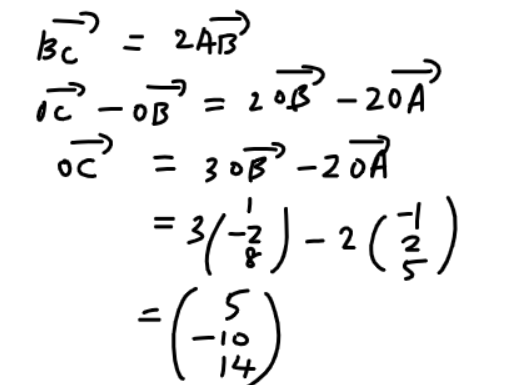
3(b)

3(c)

3(d)
In this question, we are asked to find the centre of the circle, given 3 points on the circle.
There are many ways to solve this question, but you’ll need to make use of some properties of circles you have learned in O Level Math to solve this.
The property that I’ll be using for circles is:
- Perpendicular bisector of chord
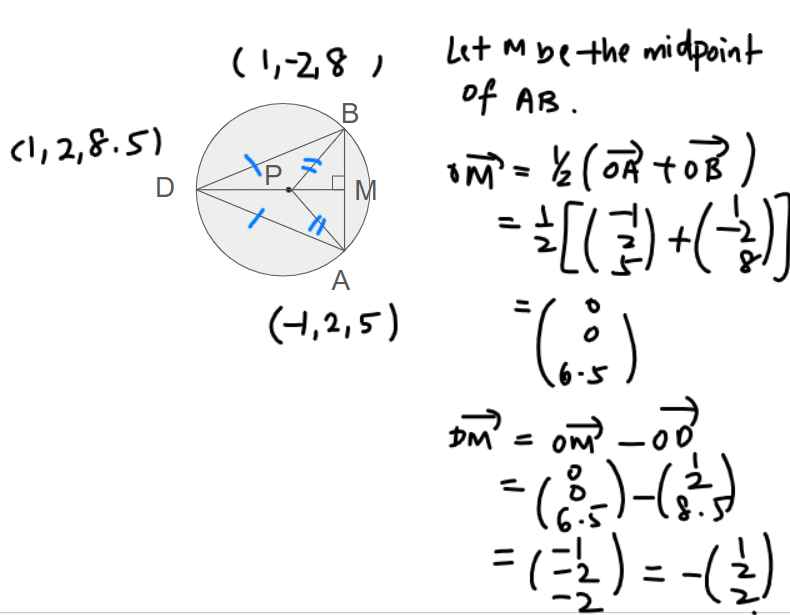



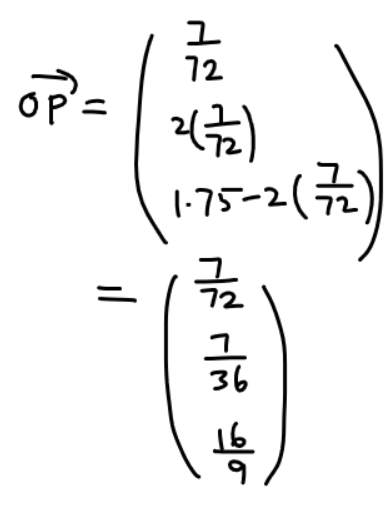
Watch the video explanation of this question here: https://youtu.be/1fDt9vXlGzs
Question 4
This is a question on integration.
(a)


(b)

(c)
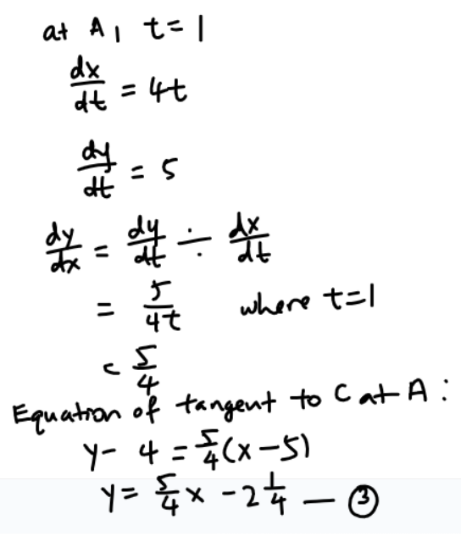

Section B of 2023 A Level H2 Mathematics (Statistics)
Question 5
This is a question on probability
(a) (i) A and B, A and D are mutually exclusive
(ii) For A and C to be independent, P(A) x P(C) = P(A∩C)
P(A) = 1/2
P(C) = 12/36 = 1/3
P(A∩ C) = 6/ 36 = 1/6
Since P(A) x P(C) = 1/2 x 1/3 = 1/6 = P(A∩C), hence A and C are independent.
(b)
(i) A and B, A and D are mutually exclusive
(ii) In numbers 1 to 35, there are 18 odd number and 17 even numbers.
P(A) = 18/35
P(C) = 11/35 [since there are 11 multiples of 3 from 1 to 35]
P(A∩C) = 6/36 = 1/6
P(A) x P(C) = 18/35 x 11/35 = 198/1225 ≠P(A∩C)
Hence, A and C are not independent.
Question 6
This question is on probability and permutation and combination.
(a)
Number of ways where there are 4 red counters and 8 blue counters removed = (ʳC₄)(ᵇC₈)
Number of ways where there are 3 red counters and 9 blue counters removed = (ʳC₃)(ᵇC₉)
P(4 red counters removed) = P( 3 red counters removed)
(ʳC₄)(ᵇC₈)/ total number of ways = (ʳC₃)(ᵇC₉)/ total number of ways
(ʳC₄)(ᵇC₈) = (ʳC₃)(ᵇC₉)
Making use of this from the formula booklet:
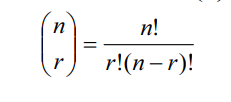

(b)
5/3 P(2 red counters removed) = P( 3 red counters removed)
[5/3 (ʳC₂)(ᵇC₁₀)]/ total number of ways = (ʳC₃)(ᵇC₉)/ total number of ways

Question 7
This question is on correlation and linear regression
(a) (i)
r= 0.928127 =0.9281 (4 d.p)
(ii)
r= 0.969723 = 0.9697 ( 4 d.p)
(b)
eʸ = cx+ d is a better fit, since r is closer to 1.
eʸ= 375.615x – 1881.481
(c)
In 2024, x = 24
eʸ= 375.615(24) – 1881.481
y= 8.87252= 8.87 (3 s.f.)
In 2024, there are 8.87 million subscribers
This estimate is not reliable, as we are doing an extrapolation. When estimating for year 2024, x = 24, which is out of the range of data of x used to obtain the linear regression model.
Question 8
This question is on hypothesis testing.
(a)(i)
H₀: µ = 1 kg
H₁: µ ≠ 1 kg
Parameters used
µ : population mean mass of a bag of granulated sugar
H₀: null hypothesis
H₁: alternative hypothesis
(ii)
We do not have information on the type of distribution of the mass of a bag of sugar.
The number of samples is 10, which is small. Hence, we are not able to use Central Limit Theorem to approximate the mean mass of a bag of sugar to normal distribution.
(b)
(i)

H₀: µ = 2 kg
H₁: µ < 2 kg
Since n = 40 is large, under H₀, x̄~N (µ, s²/n) approximately by Central Limit Theorem.
At 2.5% level of significance, critical region: z <-1.96 (3 s.f.)
(ii)
zₜₑₛₜ = -3.15024 = -3.16 (3 s.f.)
Since zₜₑₛₜ = -3.16 lies within the critical region, we reject H₀ at the 2.5% level of significance, and conclude that there is sufficient evidence that the mean mass of a bag of sugar is lesser than 2 kg.
Question 9
This question is on normal distribution.
(a)
Let L be the mass of long planks in metres.
L~N(1.82, 0.2²)
P(L<1.79) = 0.440382 = 0.440 (3 s.f.)
(b)
Let T = L₁+L₂+L₃+…+L₈
E(T) = 8(1.82) = 14.56
Var(T) = 8(0.2)² = 0.32
T~N(14.56, 0.32)
P(T>14.5) = 0.542235 = 0.542 ( 3 s.f.)
(c)
Let R be the length of a regular plank in metres.
R ~ N(1.22, 0.3²)
P(R>1.25) = 0.460172
Expected number of planks with length greater than 1.25 m = 0.460172 (120) = 55.22 = 55 ( nearest whole number)
(d)
Let X be the total length of 10 long planks. X~N(18.2, 0.4)
Let Y be the total length of 16 regular planks. Y~ N(19.52, 1.44)
Y- X ~N(19.52-18.2, 0.4 + 1.44)
Y-X~ N(1.32, 1.84)
P(|Y-X|<0.65) = P(-0.65<Y-X < 0.65) =0.23746 = 0.237 (3 s.f.)
(e)
Let V be the length of a short plank made from a long plank.
V= 1/3L
E(V) = 1.82/3 = 91/150
Var(V) = (1/3)²(0.2²) = 1/225
V~N(91/150, 1/225)
Let W be the length of a short plank made from a regular plank.
W = 1/2 R
E(W) = 1/2 (1.22) = 0.61
Var(W) = (1/2)²( 0.3)² = 0.0225
W ~ N(0.61, 0.0225)
V-W ~N(91/150 – 0.61, 1/225- 0.0225)
V-W ~N(- 1/300, 97/3600)
P(V-W>0) = 0.491899 = 0.492 ( 3 s.f.)
(f)
Cutting 3 short planks from a long plank is likely to involve more wastage, compared to cutting 2 short planks from a regular planks. Hence, the probability of V being greater than W is likely to be lower than that calculated in (e).
Question 10
This question is on binomial distribution.
(a)(i)
(i) The event that any glass ornament is faulty, is independent of other glass ornaments.
The probability that the glass ornament is faulty is the same or constant for all glass ornaments.
(ii)
Let X be the number of faulty glass ornaments out of 50 glass ornaments produced.
X~ B(50, 0.04)
E(X) = 50 (0.04) = 2
Var(X) = 50(0.04)(1-0.04) = 1.92
E(X) – Var(X) = 2 – 1.92 = 0.08 [shown]
(iii)
P(X≤2) = 0.676714 = 0.677 (3 s.f.)
(iv)
Let Y be the number of days out of 5 where no more than 2 faulty ornaments are produced.
Y~B(5, 0.676714)
P(Y≥ 3) = 1- P(Y≤2) = 0.80478 = 0.805 ( 3 s.f.)
(v)
Let W be the number of faulty glass ornaments out of 250 glass ornaments produced.
W~ B(250, 0.04)
P(W≤10) = 0.583057 = 0.583 (3 s.f.)
(b)
Let L be the number of pens out of 6 that are faulty. L ~ B(6, 1-p)
Let M be the number of pens out of 3 that are faulty. M ~B(3, 1-p)
P(Mr Lu accepts the box of pen)
= P(L = 0) + P(L = 1)
= p⁶ + 6p⁵(1-p)
= p⁶ – 6p⁶ + 6 p⁵
= 6 p⁵ – 5p⁶
P(Mrs Ming accepts the box of pen) = P(M = 0) + P(M=1) P(M = 0) = p³ +3p²(1-p)p³ = p³ +3p⁵- 3p⁶
P(Mrs Ming accepts the box of pen) – P(Mr Lu accepts the box of pen)
= (p³ +3p⁵- 3p⁶) -( 6 p⁵ – 5p⁶)
= p³ – 3p⁵ + 2p⁶
=p³(1-3p²+2p³)
=p³(p-1)²(2p+1)
Since 0<p<1, 0<p³<1
(p-1)² is positive for 0<p<1
1<2p+1<3
Since p³, (p-1)² and 2p+1 are positive, p³(p-1)²(2p+1) is also positive.
P(Mrs Ming accepts the box of pen) – P(Mr Lu accepts the box of pen) > 0
Hence, P(Mrs Ming accepts the box of pen) > P(Mr Lu accepts the box of pen) [shown]
The full explanation video question 10b can be found here: https://youtu.be/XgBD736r1Dg
For other H2 A Level Math Worked solutions
- Syllabus 9758 Specimen Paper 2025 Paper 2
- Syllabus 9758 Specimen Paper 2025 Paper 1
- Syllabus 9758 Year 2023 Paper 1
- Syllabus 9758 Year 2023 Paper 2
- Syllabus 9758 Year 2022 Paper 1
- Syllabus 9758 Year 2022 Paper 2
- Syllabus 9758 Year 2021 Paper 1
- Syllabus 9758 Year 2021 Paper 2
- Syllabus 9768 Year 2020 Paper 1
- Syllabus 9758 Year 2020 Paper 2
- Syllabus 9758 Year 2019 Paper 1
- Syllabus 9758 Year 2019 Paper 2
- Syllabus 9768 Year 2018 Paper 1
- Syllabus 9758 Year 2018 Paper 2
Learn H2 Math on-demand with our online courses
Find a list of our H2 Math Resources here.
