2022 H2 A Level Mathematics Paper 1 Worked Solutions

Here’s the worked solutions for the 2022 H2 A Level Mathematics Paper 1. Click on the question number to go to the question directly.

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Worked solutions for 2022 H2 A Level Mathematics Paper 1

Question 1

Given :

iz + 2w = -1 —- (1)

(2-i)z + iw = 6 —- (2)

Find z and w in a + bi form where a and b are real numbers.

Question 2

This is a question on Maclaurin Series.

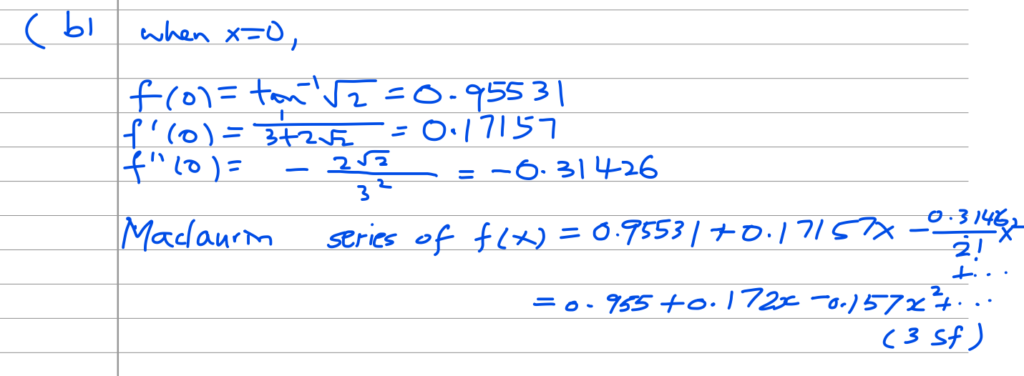
Question 3

This question is on application of differentiation to tangents and normals.

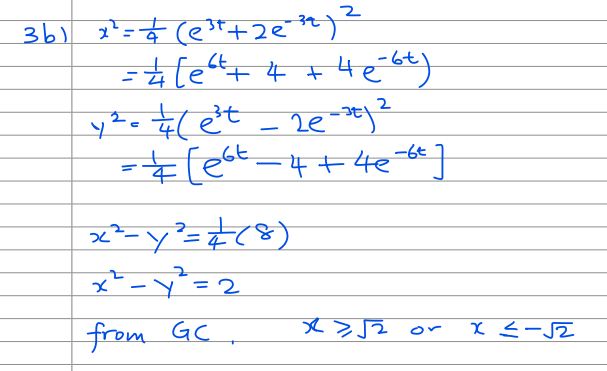
Question 4

This question tests students on manipulating Trigonometric identities, and also on integration.

Question 5

This question tests students on their application of differentiation. In addition, concepts from O Level Additional Mathematics topics on discriminant (from quadratic function chapter) is also tested.

Question 6

Question 6 is on functions and transformation of graphs.

(a)

Students are expected to write a series of transformation to transform y = 1/x to y = (ax+k)/(x-a). Remember to use the recommended transformation order for this question.

Hence, the required transformation are:

• translate the graph y = f(x) a units in the positive x- direction.
• scale parallel to the y axis by a factor of a² + k
• translate the graph by a units in the positive y- direction

(b)

Let y = f(x)

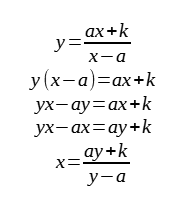
Range of f = domain of f⁻¹ = ℝ \ a

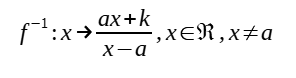
(c )

Since f(x) = f⁻¹(x),

f²(x) = f f⁻¹(x) = x, x ∈ ℝ, x ≠a

(d)

f²⁰²³(1) = f(1) = (a+k)/(1-a)

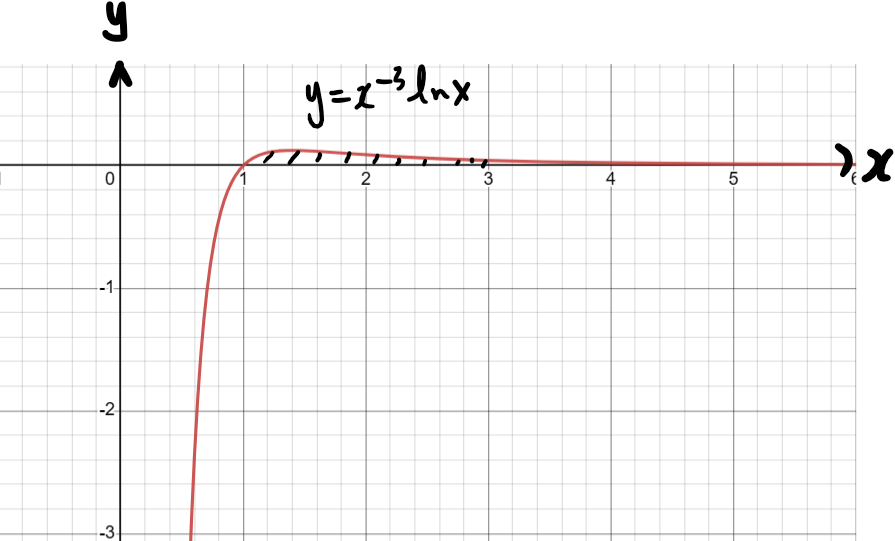
Question 7

Question 7 is on differentiation and integration (including their application)

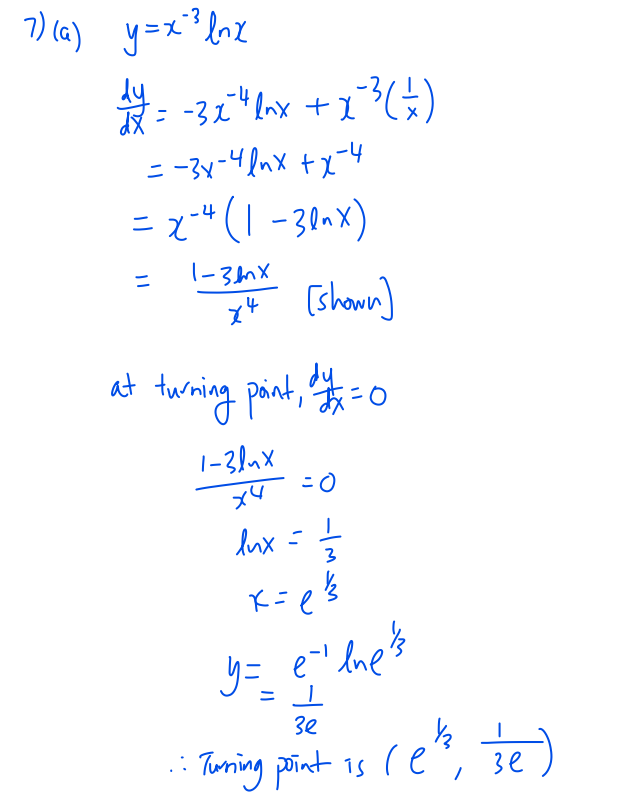
(b)

Question 8

Question 8 is on integration and its application.

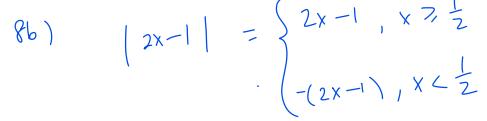
Question 9

Question 9 is on arithmetic and geometric progression.

Question 10

Question 10 is on application of differentiation, discriminant, curve sketching and inequalities.

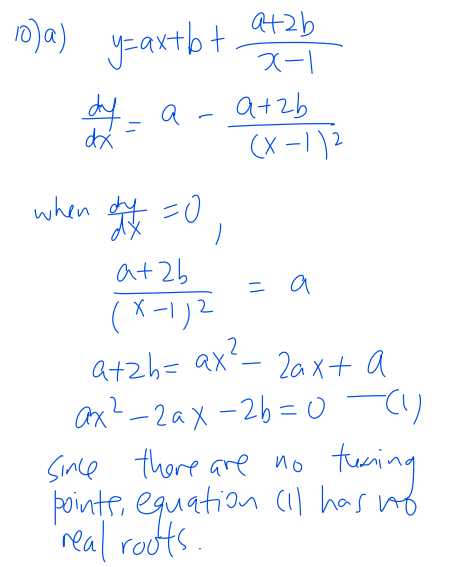
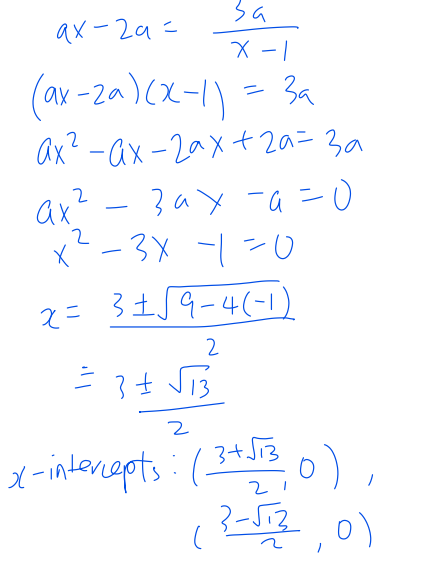
Question 11

This question is on vectors.

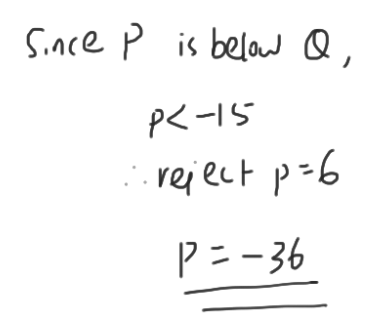
(b)

Part b involves finding the cartesian equation of plane, given 3 position vectors:

Question 12

This question is on differential equations.

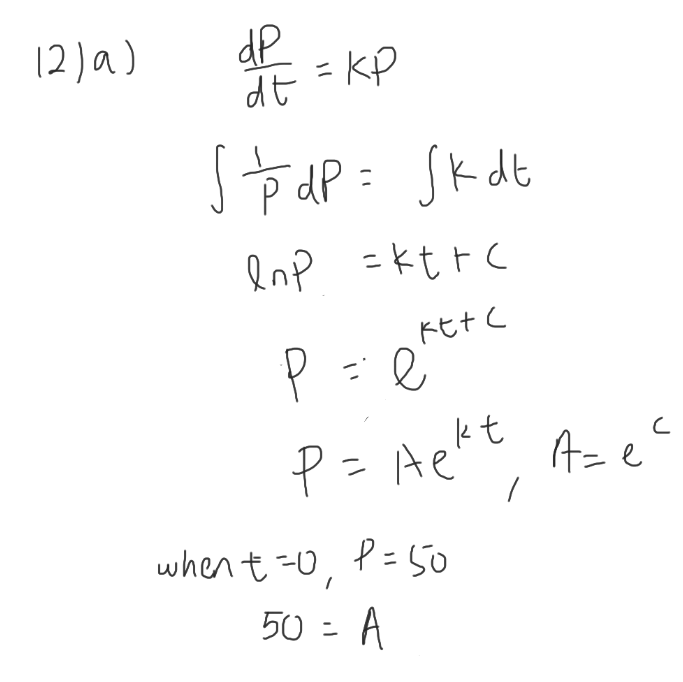
For other H2 A Level Math Worked solutions

• Syllabus 9758 Specimen Paper 2025 Paper 2
• Syllabus 9758 Specimen Paper 2025 Paper 1
• Syllabus 9758 Year 2023 Paper 1
• Syllabus 9758 Year 2023 Paper 2
• Syllabus 9758 Year 2022 Paper 1
• Syllabus 9758 Year 2022 Paper 2
• Syllabus 9758 Year 2021 Paper 1
• Syllabus 9758 Year 2021 Paper 2
• Syllabus 9768 Year 2020 Paper 1
• Syllabus 9758 Year 2020 Paper 2
• Syllabus 9758 Year 2019 Paper 1
• Syllabus 9758 Year 2019 Paper 2
• Syllabus 9768 Year 2018 Paper 1
• Syllabus 9758 Year 2018 Paper 2

Learn H2 Math on-demand with our online courses

• H2 A Level Statistics

Find a list of our H2 Math Resources here.