2018 H2 A Level Mathematics Paper 2 Worked Solutions

Here’s the worked solutions for the 2018 H2 A Level Mathematics Paper 2. Click on the question number to go to the question directly.

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Worked solutions for 2018 H2 A Level Mathematics Paper 2

Question 1

This question is on differential equations.

Question 2

This is a question on complex numbers.

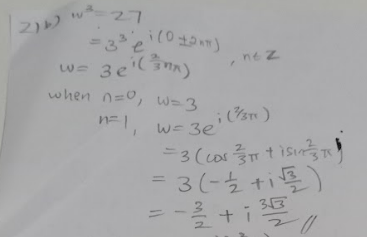
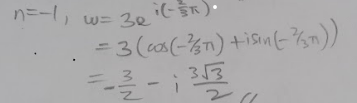
Question 3

This question is on vectors.

Question 4

This question is on Maclaurin’s series.

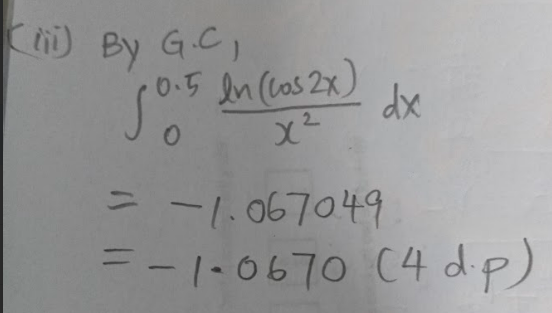
Question 5

This question is on sampling and hypothesis testing.

(i) A sample of at least 30 should be taken, so that sample size is large enough for the mean time to fail of the fans to be approximated to that of a normal distribution by Central Limit Theorem.

(ii) Test H_o: µ = 65000 against H₁: µ < 65000

µ = population mean time to fail of fan

H_o = null hypothesis

H₁ = alternative hypothesis

Question 6

This question is on probability.

(i) By observation, it’s observed that no matter which route is taken to reach D, it involves 8 steps, 3 of them are right fork and 5 of them are left fork.

Probability that bug finishes at D = 8! / (3!5!) p⁵q³ = 56p⁵q³ [shown]

(ii) Let X be the number of left forks made out of 8. X~B(8, p)

Given probability at D = P(X= 5) is maximum for this binomial distribution,

we know that P(X =5) > P(X =6) and P(X= 5) > P(X=4)

56p⁵(1-p)³ >⁸C₆ p⁶(1-p)²

56p⁵(1-p)³ > 28p⁶(1-p)²

2(1-p)- p > 0

2-3p > 0

p<2/3

and

56p⁵(1-p)³ >⁸C₄ p⁴(1-p)⁴

56p⁵(1-p)³ >70p⁴(1-p)⁴

4p – 5(1-p) > 0

p>5/9

Hence 5/9 <p <2/3

(iii) To reach any endpoint at A- I, bug will take 8 moves.

In each move, probability that bug is not swallowed by black hole = 1 – 0.1 = 0.9

To reach A-I without being swallowed by black hole, for all 8 moves, bug must not be swallowed by black hole.

Required probability = (0.9)⁸ = 0.43046721

Note: This question can be done as a binomial distribution. Part (ii) is testing students on mode of binomial distribution.

Question 7

This question is on probability.

This probability question is best down using either formulae and/ or sketching of Venn diagrams.

(i) Since A and B are independent, P(A∩B) = P(A) x P(B) = ab

P(A’∩B’) = 1 – P(AUB) = 1- [a + b – ab] = 1- a-b+ ab

P(A’) = 1- a; P(B’) = 1 -b

P(A’)xP(B’) = (1-a)(1-b) = 1-a-b+ab = P(A’∩B’)

Since P(A’) x P(B’) = P(A’∩B’), A’ and B’ are independent events. [shown]

(ii) Since A and C are mutually exclusive, P(A∩C) = 0

P(A’∩C’) = 1 – a – c

(iii) Given A’ and C’ are not mutually exclusive,

based on information from the first part, P(A) and P(B) are independent –> P(A)P(B) = P(A∩B)

max P(A∩B) = 2/15

min P(A∩B) = 1/3

Question 8

(i) two 3, three 4, n 5.

Possible values of S:

ball 1 /ball 2	3	4	5
3	6	7	8
4	7	8	9
5	8	9	10

S	6	7	8	9	10
P(S=s)	2/ [(n+4)(n+5)]	12/ [(n+4)(n+5)]	(6+4n)/[(n+4)(n+5)]	6n/[(n+4)(n+5)]	n(n-1)/[(n+4)(n+5)]

(ii) when n = 1, P(S=10) = 0

There is no possibility that S = 10. In order for S=10, two balls numbered 5 have to be picked. However, since there is only 1 ball numbered 5, it is not possible to pick 2 balls numbered 5 (without replacement).

(iii) E(S) = 12/ [(n+4)(n+5)] +84/ [(n+4)(n+5)] +(48+32n)/[(n+4)(n+5)] + 54n/[(n+4)(n+5)] +10n/(n-1)/[(n+4)(n+5)] =(144+76n+10n²)/[(n+4)(n+5)] =2(n+4)(5n+18)/[(n+4)(n+5)] = (10n+36)/[(n+5)]

E(S²) = 72/ [(n+4)(n+5)] +588/ [(n+4)(n+5)] +(384+256n)/[(n+4)(n+5)] + 486n/[(n+4)(n+5)] +100n/(n-1)/[(n+4)(n+5)] =(1044+642n+100n²)/[(n+4)(n+5)]

Var(S) =E(S²) – [E(S)]² = (1044+642n+100n²)/[(n+4)(n+5)] – (10n+36)²/[(n+5)²]

= [(1044+642n+100n²)(n+5) -(100n²+720n+1296)(n+4)]/ [(n+4)(n+5)²]

= [22n² + 78n + 36]/ [(n+4)(n+5)²]

g(n) = 22n² + 78n + 36

Question 9

This question is on correlation and linear regression.

(i) Scatter diagram:

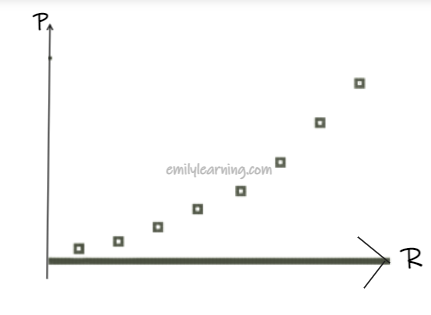
From scatter plot shows that the relationship between P and R is non- linear. Hence, P and R may not be well modelled with the linear equation of P = aR + b

(ii)

For model P = aR + b, r = 0.96929 = 0.970 ( 3 s.f.), b = -1.41857 = -1.42 (3 s.f.), a = 3.78306 = 3.78 ( 3 s.f.)

For model P = aR²+b, r = 0.9930388 = 0.993 ( 3 s.f.), b = -0.282607 = -0.283 ( 3 s.f.), a = 2.84577 x 10 ^-8 =2.85 x 10^-8

Since P = aR²+b has an r value closer to 1, it is a better model.

(iii) P = (2.84577 x 10 ^-8)R² – 0.282607

when P = 0.9, R = 6446.4 = 6450 (3 s.f.)

Estimation is reliable as r is close to 1, and P -= 0.9 is within the data range.

(iv) when R= 3300, P = 0.027297 = 0.0273 ( 3 s.f.)

Estimation is unreliable, as we are doing an extrapolation.

(v) P = 3600[(2.84577 x 10 ^-8)R² – 0.282607]

Question 10

This question is on normal distribution.

(i) Let the mass of the light bulb be X.

X~ N(50, 1.5²)

Using the graphic calculator, P(40<X<60) = 1

(ii) P(X<50.4) = 0.605137 = 0.605 (3 s.f.)

(iii) Let the mass of an empty box be B grams

B~N(75, 2²)

Let T = B₁ + B₂ + B₃ + B₄

T~ N(300, 16)

P(T > 297) = 0.77337 = 0.773 ( 3 s.f.)

(iv) Let W = B + X

W~ N(125, 6.25)

P(124.9 < W < 125.7) = 0.126214 = 0.126 (3 s.f.)

(v) Let Y be the total mass of the bulb, padding and box in grams.

Y = 1.3X + B

Y~ N(1.3(50)+75, 1.3²(1.5²) + 2²) = N(140, 7.8025)

P(Y>k) = 0.9

k = 136.420 = 136 ( 3.s.f)

(vi) Let C = Y₁ + Y₂ + Y₃ + Y₄

C~ N(140 x 4 , 7.8025 x 4) = N(560, 31.21)

P(C>565) = 0.185393 = 0.185 ( 3 s.f.)

For other H2 A Level Math Worked solutions

• Syllabus 9758 Specimen Paper 2025 Paper 2
• Syllabus 9758 Specimen Paper 2025 Paper 1
• Syllabus 9758 Year 2023 Paper 1
• Syllabus 9758 Year 2023 Paper 2
• Syllabus 9758 Year 2022 Paper 1
• Syllabus 9758 Year 2022 Paper 2
• Syllabus 9758 Year 2021 Paper 1
• Syllabus 9758 Year 2021 Paper 2
• Syllabus 9768 Year 2020 Paper 1
• Syllabus 9758 Year 2020 Paper 2
• Syllabus 9758 Year 2019 Paper 1
• Syllabus 9758 Year 2019 Paper 2
• Syllabus 9768 Year 2018 Paper 1
• Syllabus 9758 Year 2018 Paper 2

Learn H2 Math on-demand with our online courses

• H2 A Level Statistics

Find a list of our H2 Math Resources here.