2022 H2 A Level Mathematics Paper 2 Worked Solutions

Here’s the worked solutions for the 2022 H2 A Level Mathematics Paper 2. Click on the question number to go to the question directly.

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Worked solutions for 2022 H2 A Level Mathematics Paper 2

Question 1

This question is on integration by substitution.

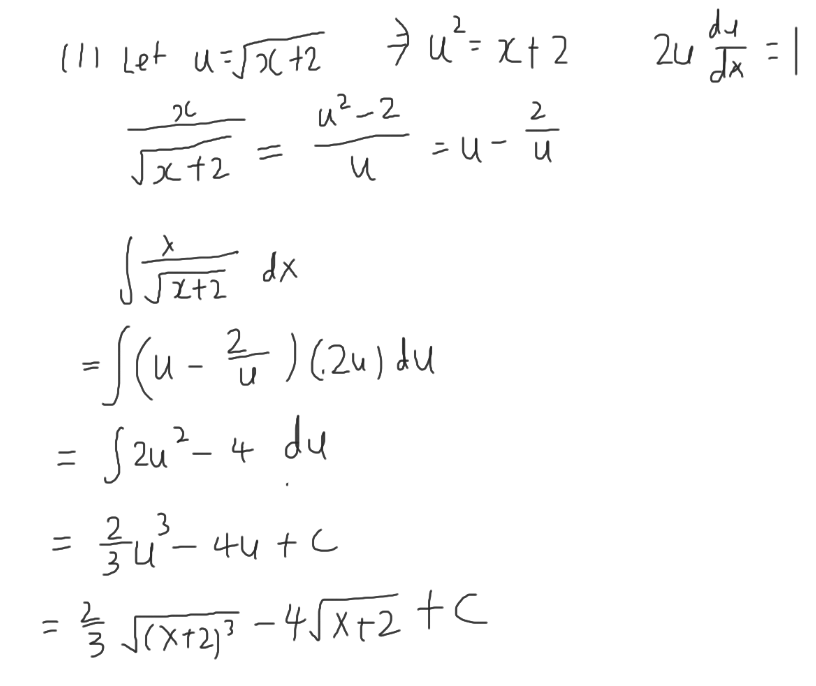
Question 2

This question is on differential equations.

(a)

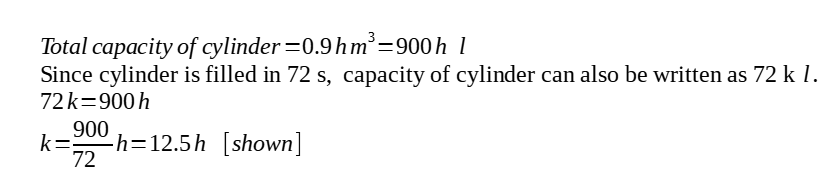
(b)

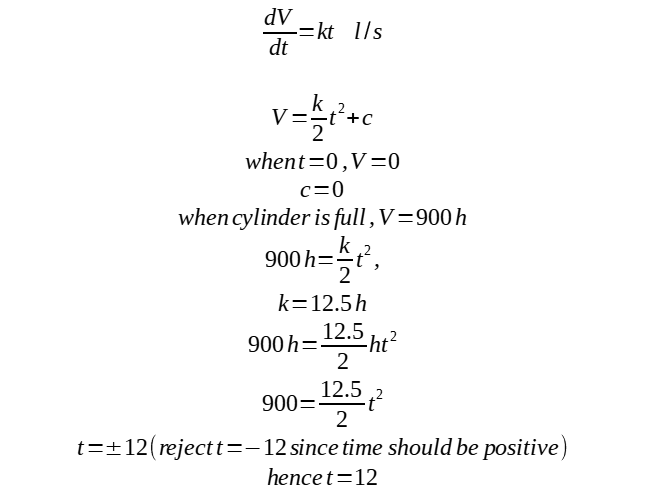
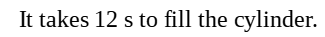
(c)

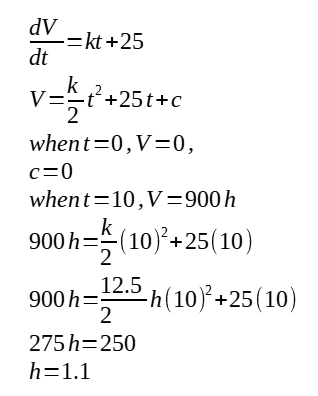
Question 3

This question is on complex numbers.

3(a)

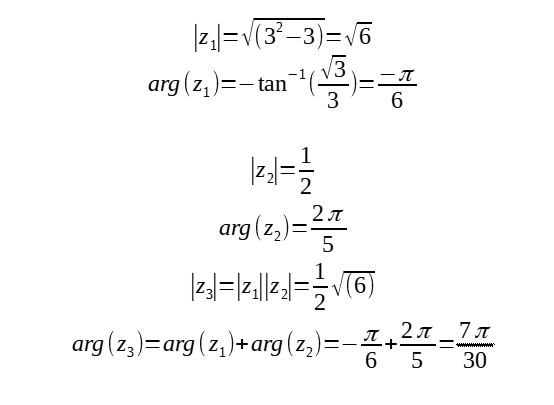
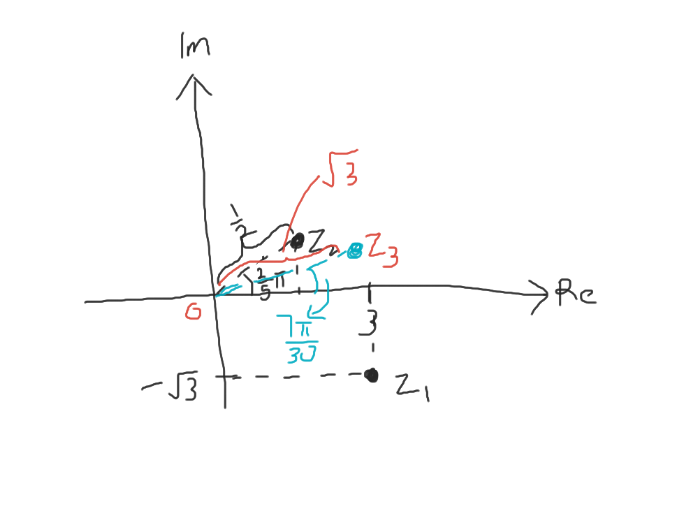
3(b) Plotting z₁, z₂ and z₃ on an argand diagram:

3(c)

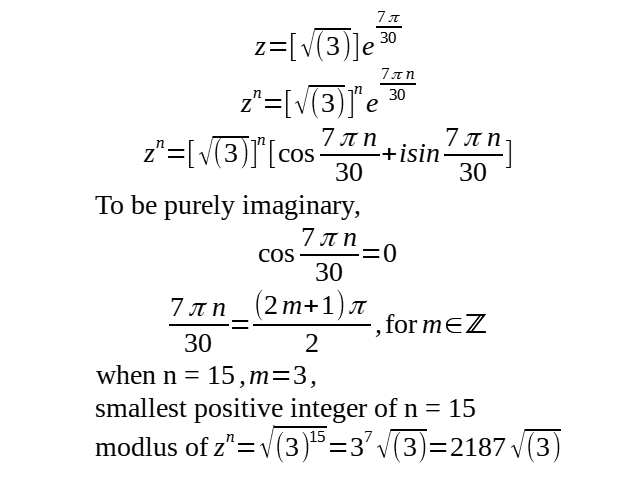
Hence k = 2187

Question 4

This is a question on summation using method of difference.

(a)

(b)

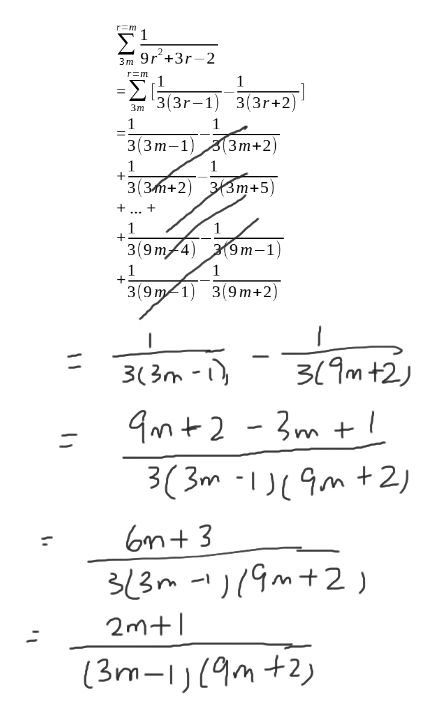
(c)

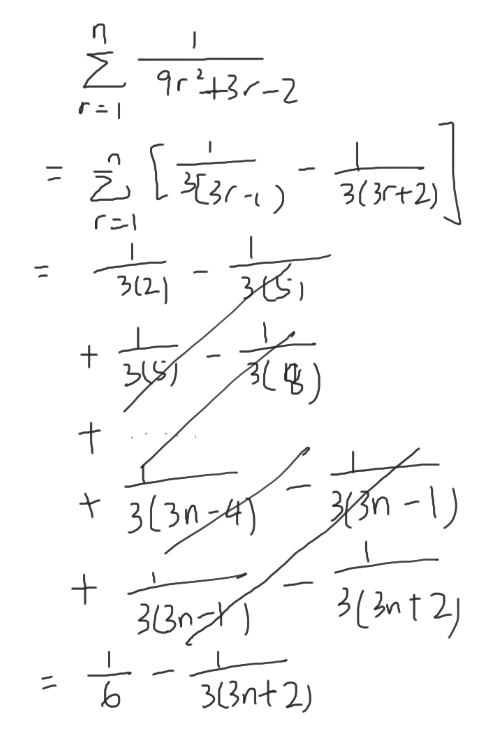
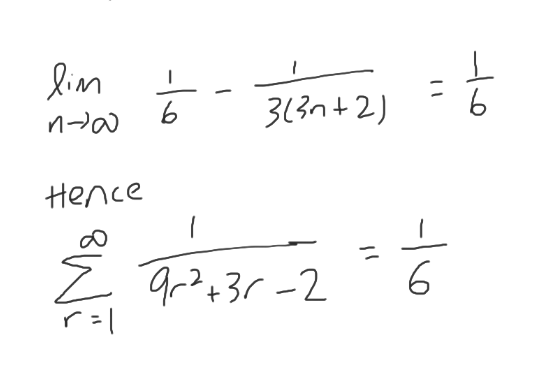
(d)

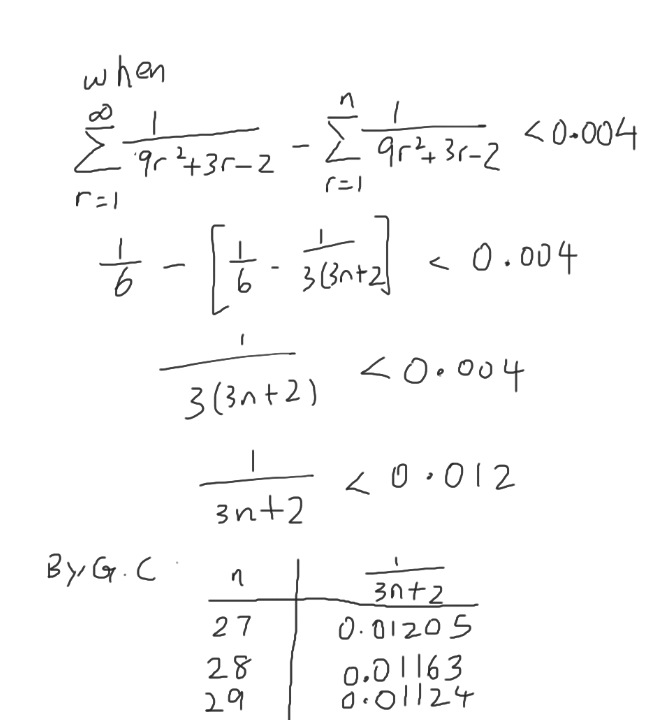
Hence, smallest n value = 28

Question 5

This is a question involving application of integration.

(a)

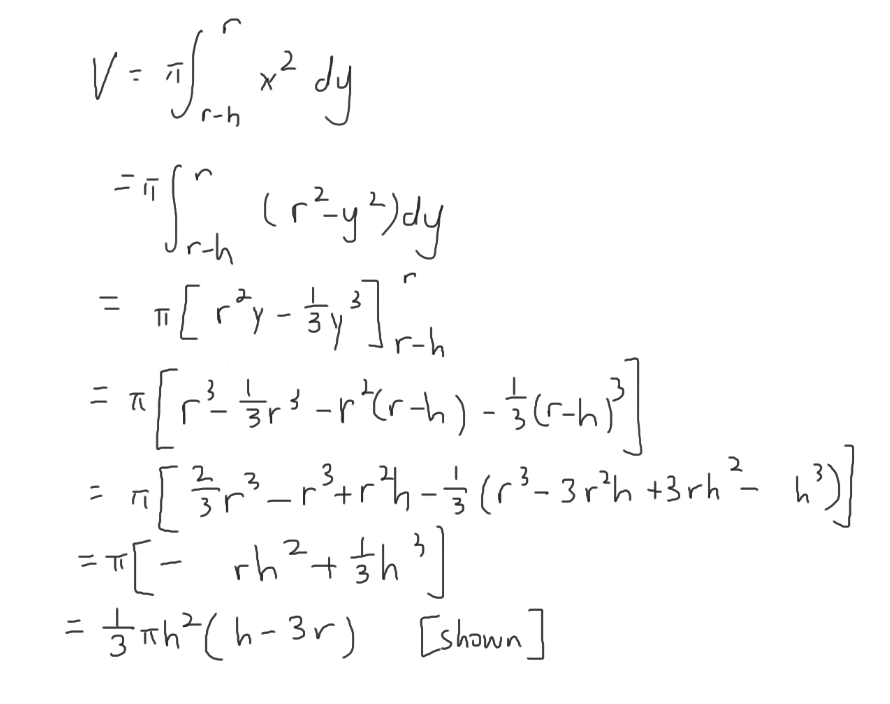
(b)

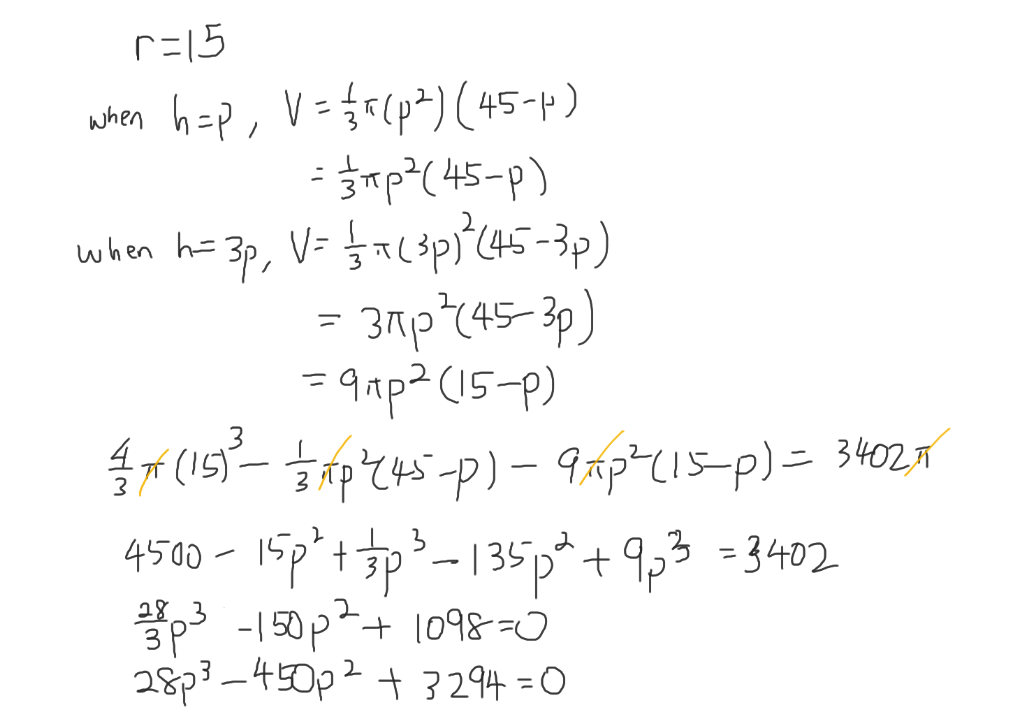
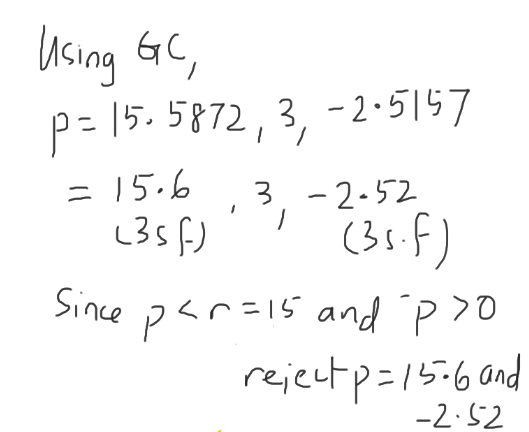
Hence, r = 3 cm

(c)

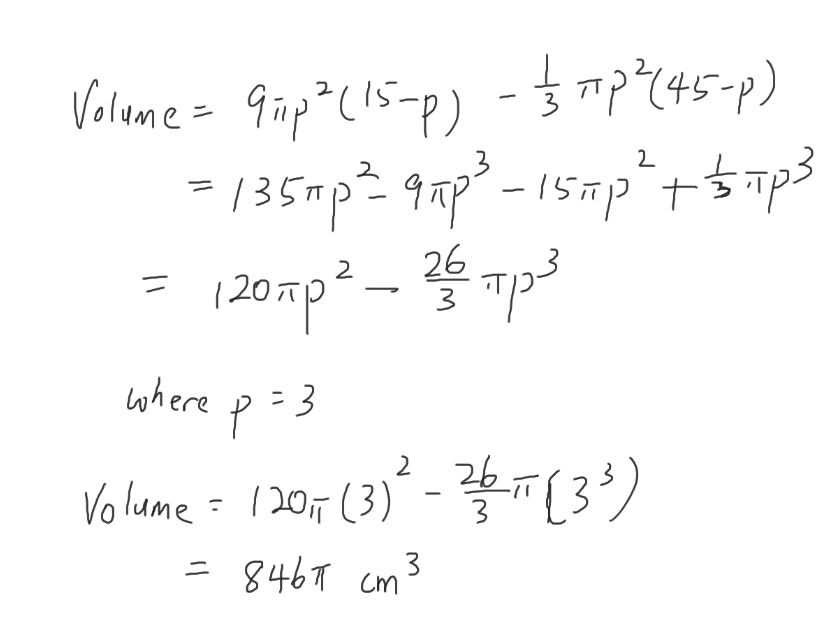
Question 6

This is a question on probability.

(a) Required probability = (1)(5/6)(1/6) + (1)(5/6)(5/6)(5/6)(1/6)+(1)(5/6)(5/6)(5/6)(5/6)(5/6)(1/6) + …

= 5/36[1+(5/6)² + (5/6)⁴+…]

=5/36 [ 1/ (1-(5/6)²)]

=5/11

(b)

P(Babs wins on second throw) = (1)(5/6)(5/6)(1/6) = 25/216

P(Babs wins) = 1 – 5/11 = 6/11

P(Babs wins on second throw | Babs wins) = 25/216 / 6/11 = 275/1296

Question 7

This question is on permutation and combination and questions on samples.

(a) This 53 people forms part of the 75 employees in Staffing. Hence, they are a sample.

(b) She should use a sample by picking employees randomly from each department, to obtain views from the various departments. The number of employees from each department in the sample should be of the same proportion as the number of employees from each department in the company.

(c)

8 Team leaders to be selected from 4 departments, with Admin department having most people, and each department having at least 1 person.

Case 1: 5 A, and 1 from each other department

Number of ways = ⁷C₅ x ⁶C₁ x ⁴C₁ x ³C₁ = 1512

Case 2: 4A, and 2, 1, 1 from each other department

Number of ways = ⁷C₄ x ⁶C₂ x ⁴C₁ x ³C₁+⁷C₄ x ⁶C₁ x ⁴C₂ x ³C₁+⁷C₄ x ⁶C₁ x ⁴C₁ x ³C₂=12600

Case 3: 3A and 2, 2, 1 from each other department

Number of ways = ⁷C₃ x ⁶C₂ x ⁴C₂ x ³C₁ + ⁷C₃ x ⁶C₂ x ⁴C₁ x ³C₂ + ⁷C₃ x ⁶C₁ x ⁴C₂ x ³C₂ = 19530

Total number of ways = 1512 + 12600 + 19530 = 33 642

Question 8

This question is on normal distribution.

(a) Given X ~N(p, q²) and Y~N(s, t²)

aX – bY ~ N(ap -bs, a²q²+b²t²)

(b)(i) Since V is normally distributed, and P(V>8) = P(V<4), hence µ = 6

V~N(6, 4)

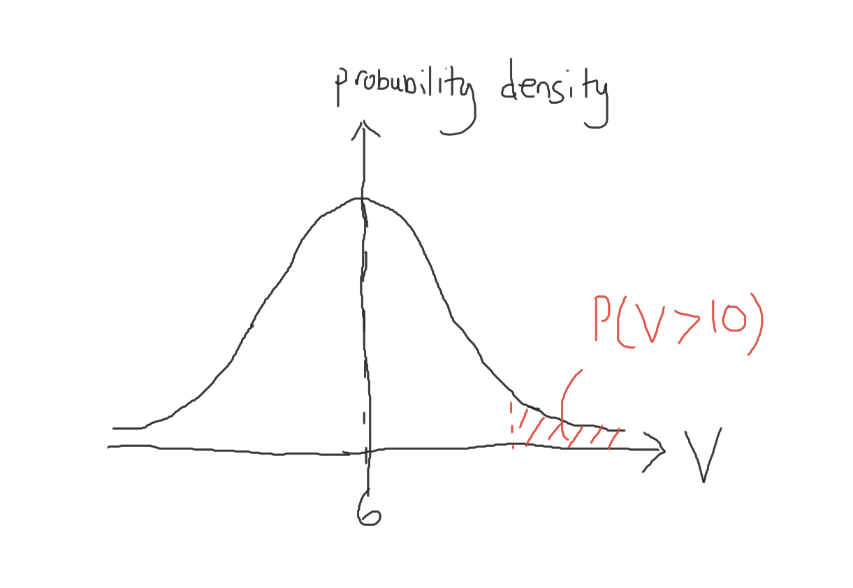
(ii) By G,C P(V>10) = 0.022750 = 0.0228 (3 s.f.)

(c)

Given W ~B(8, p)

Given E(W) = 1.2 Var(W)

8p = (1.2)8p(1-p)

p = 1.2p(1-p)

1.2p(1-p)-p = 0

p[1.2-1.2p-1]=0

p(0.2-1.2p) = 0

p = 0 OR p = 1/6

(reject p =0)

Hence, p = 1/6

P(W<2) = P(W≤1) = 0.60467 = 0.605 (3 s.f.)

Question 9

This question is on probability.

(a) To arrive at B from S, the counter needs to make 5 moves, 4 of which are left and 1 is right.

When first move is left, the other 4 moves will be 1 right and 3 left –> hence 4 ways

When first move is right, all other 4 moves must be left –> 1 way

Probability that it will arrive at B = 1/2 (4)(p³)q + 1/2 p⁴ = 2p³q + 1/2 p⁴ [shown]

(b) P (both use same route | both arrive at B)

= [(1/2)(1/2) (4)(p⁶)q² + (1/2)(1/2) p⁸ ] / [2p³q + 1/2 p⁴ ]²

= [ p⁶q² + 1/4 p⁸ ] / [2p³q + 1/2 p⁴ ]²

= [q² + 1/4p² ]/ [2q + 1/2 p ]²

= [(1-p)² + 1/4p² ]/ [2(1-p) + 1/2 p ]²

= (1-2p+5/4 p² )/ (2 – 3/2p)²

= (1- 2p +5/4 p² )/ (4 -6p + 9/4 p² )

= (4 – 8p + 5p² )/ (16 – 24p + 9p² )

(c) To arrive at C, counter makes 2 right and 3 left moves

If it starts with right, then it will make 1 other right and 3 left moves –> 4 ways

If it starts with left, then it will make 2 other right and 2 left moves —> Number of ways = 4!/(2! 2!) = 6

P(arrives at C) = 1/2 (4)(p³)q + 1/2(6) p² q² = 2p³ q + 3p² q²

Given P(arrives at C) = P(arrives at B)

2p³ q + 3p² q² = 2p³q + 1/2 p⁴ , where q = 1-p

2p³ (1-p) + 3p² (1-p)² = 2p³(1-p) + 1/2 p⁴

By G.C,

p = 0 (reject) , or p = 0.710102 = 0.710 (3 s.f.) or p = 1.689897 = 1.70 (3 s.f) –> rejected since 0<p<1

Question 10

This question is on correlation and regression.

(a) From the graph, it shows that there is a non- linear relationship between d and p.

The product moment correlation, r, between d and p is -0.78, indicating a negative relationship between d and p.

(b)

No change. The relationship between d and p still remains the same even when the units are changed.

(c) The relationship between d and p may be different for a different model.

(d)

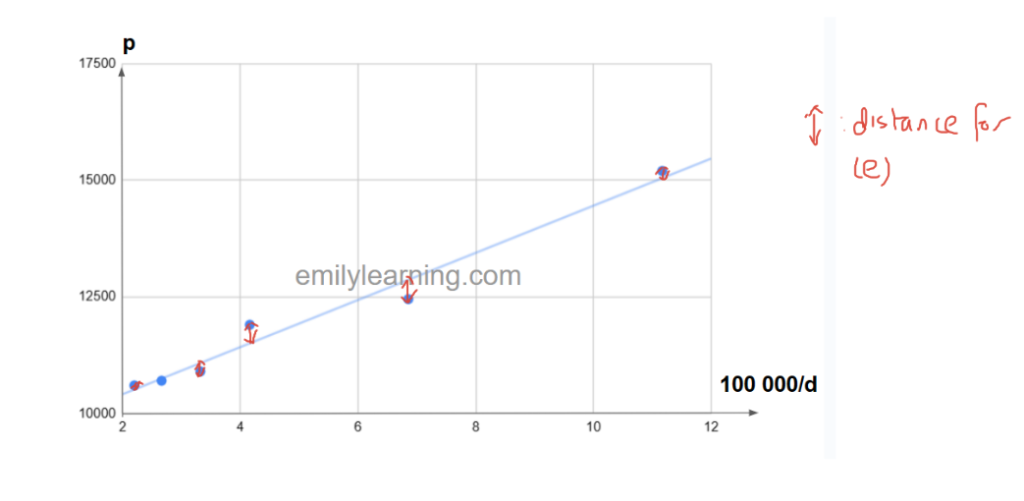
(e) Since all squared numbers are greater than or equal to zero, when the distances are squared and added together, the positive distances and the negative distances do not cancel each other out.

(f) Using G.C,

r= 0.9869962 = 0.987 ( 3 s.f.)

p = 9398.49 + 505.730(100 000/d)

p = 9400 + 506 000 000 / d (3 s.f.)

Question 11

This question is on normal distribution, sampling and hypothesis testing.

(a) Let Zhou’s timing for swimming 100 m be X seconds, and Tan’s timing for swimming 100 m freestyle be Y seconds.

X~ N(80, 2²)

Y~ N(79, 3²)

For Zhou to win, X <Y or X-Y < 0

X-Y~N(1, 13)

P(X-Y < 0) = 0.390755 = 0.391 ( 3 s.f.)

(b)

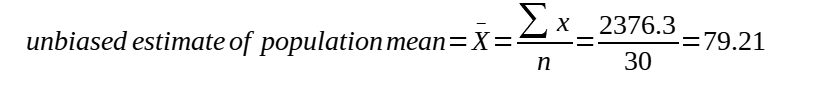
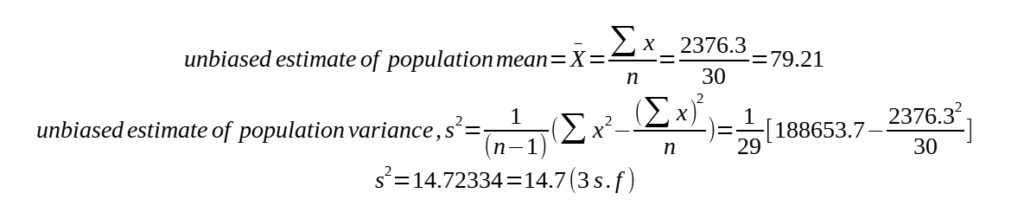
(c)

Test at 5% level of significance

H_o : µ = 80 against

H₁ : µ < 80

where H_o = null hypothesis, H₁ = alternative hypothesis, µ = population mean time of Zhou’s time for 100 m freestyle in seconds

Under H_o, X̄ ~ N (80, 4/ 30)

Test statistics,

For 1- tail test, p-value = P(Z< -2.16) = 0.015386 < 0.05

Since p-value < 0.05 (level of significance), we reject Ho at 5% level of significance, and conclude that the timing of Zhou has decreased.

(d)

2-tail test should be used.

To test whether the mean has changed, it could be an increase or a decrease. Hence, this is a 2- tailed test.

(e) The 6 samples should be representative of a high protein diet on swim times.

The time taken for the swim follows a normal distribution.

For other H2 A Level Math Worked solutions

• Syllabus 9758 Specimen Paper 2025 Paper 2
• Syllabus 9758 Specimen Paper 2025 Paper 1
• Syllabus 9758 Year 2023 Paper 1
• Syllabus 9758 Year 2023 Paper 2
• Syllabus 9758 Year 2022 Paper 1
• Syllabus 9758 Year 2022 Paper 2
• Syllabus 9758 Year 2021 Paper 1
• Syllabus 9758 Year 2021 Paper 2
• Syllabus 9768 Year 2020 Paper 1
• Syllabus 9758 Year 2020 Paper 2
• Syllabus 9758 Year 2019 Paper 1
• Syllabus 9758 Year 2019 Paper 2
• Syllabus 9768 Year 2018 Paper 1
• Syllabus 9758 Year 2018 Paper 2

Learn H2 Math on-demand with our online courses

• H2 A Level Statistics

Find a list of our H2 Math Resources here.