In this post, we’ll look at solving inequalities involving modulus function, and the modulus function is limited to “part” of the expression on either (or both sides ) of the inequality sign.
Examples of such inequalities include:
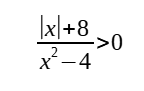
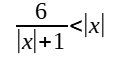
For such questions, you do not have a single | | on either side or both sides of the inequality sign. However, you have the | | only over certain terms e.g. x. To solve such inequalities, let y = |f(x)|, and solve for y. Once y is solved, you can solve for x.
Example 1:
Solve the following inequality
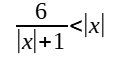
Solutions
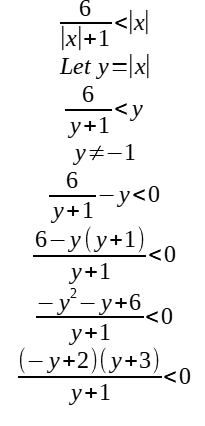
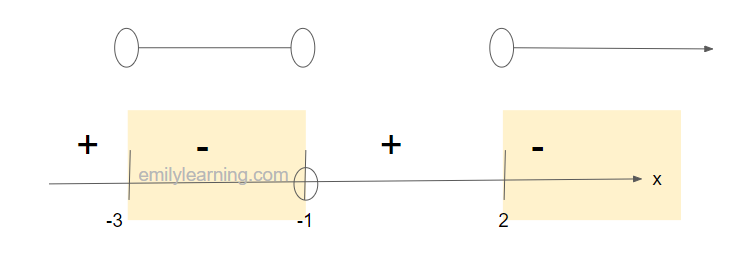
-3<y < -1 or y > 2
Since y = |x|,
-3<|x|<-1 (reject, since |x|≥ 0 for all values of x) OR |x| > 2 ==> x > 2 or x < -2
Hence, x > 2 or x < -2.
Example 2:
Solve the following inequality
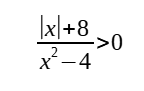
Solutions
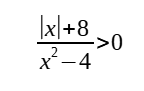
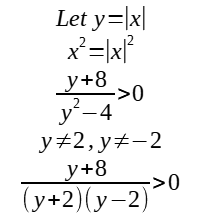
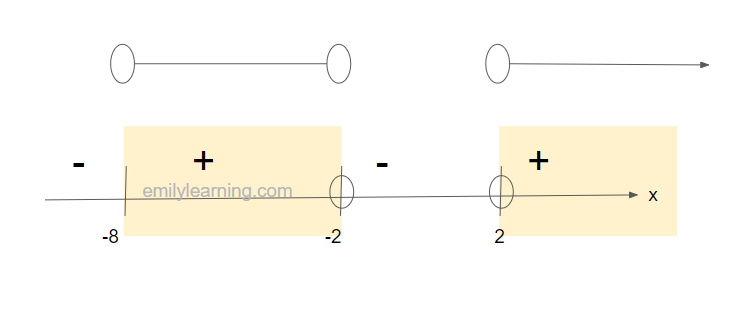
-8<y<-2 or y> 2
Since y = |x|,
-8<|x|<-2 (reject since |x| ≥ 0 for all values of x) OR |x| > 2==> x> 2 or x < -2
Hence, x> 2 or x < -2
Learn H2 A Level Math Inequalities
Here are the complete notes for solving inequalities for H2 Math:
- Solving inequalities using the graphic calculator
- Solving inequalities involving polynomials
- Solving inequalities involving polynomial fractions
- Quadratic functions that are always positive or negative
- Solving inequalities with functions that are always positive or negative
- Modulus Functions
- Solving inequalities involving modulus functions 1
- Solving inequalities involving modulus functions 2
- Solving inequalities involving modulus functions 3
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
