What are modulus functions
Modulus functions or absolute functions give the magnitude (and ignore the negative sign). Hence, a modulus function is always greater than or equal to 0.
Representing modulus functions in Math
To represent modulus functions, we use the symbol | |.
Examples of modulus functions
|-3|, |x+3|, |(x-3)(x+5)| ,etc. are examples of modulus functions.
Example 1: |-3| = 3
Reason: since modulus functions only take the magnitude, and ignore any negative sign.
Example 2: |3| , |3| = 3.
Notice that |3| =|-3| = 3.
Splitting the modulus function
Using the example of |3| = 3 and |-3| = 3, notice that:
- when f(x) ≥0, |f(x)| = f(x).
- when f(x)<0, then |f(x)| = -f(x)
Hence, when we have a modulus function, we can split it in this manner:

For example, |x-3| can be re-written in the form:
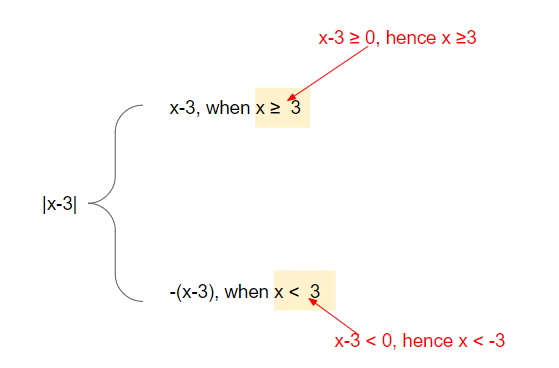
Learn H2 A Level Math Inequalities
Here are the complete notes for solving inequalities for H2 Math:
- Solving inequalities using the graphic calculator
- Solving inequalities involving polynomials
- Solving inequalities involving polynomial fractions
- Quadratic functions that are always positive or negative
- Solving inequalities with functions that are always positive or negative
- Modulus Functions
- Solving inequalities involving modulus functions 1
- Solving inequalities involving modulus functions 2
- Solving inequalities involving modulus functions 3
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
