Solving Inequalities with modulus sign: |f(x)| < g(x) or |f(x)| > g(x)

In this post, we’ll look at solving inequalities of the form |f(x)| < g(x) or |f(x)| > g(x).

How to remove the | |

To solve such inequalities, we’ll first look at how to split such inequalities:

• If given |f(x)| < g(x), split it into -g(x)<f(x) < g(x) [Take the intersection of both to find final answer]
• Similarly, if given |f(x)| ≤ g(x), split it into -g(x)≤f(x)≤g(x) [Take the intersection of both inequalities to find final answer]
• If given |f(x)| > g(x), split it into f(x) > g(x) or f(x) < -g(x) [Take both inequalities as final answer]
• Similarly, if given |f(x)| ≥ g(x), split it into f(x)≥ g(x) or f(x)≤-g(x) [Take both inequalities as final answer]

---

Examples of solving inequalities involving | |

Example 1: Solve the inequality |x – 3| < 2x + 5

If given |f(x)| < g(x), split it into -g(x)<f(x) < g(x)

Hence, we’ll split |x – 3| < 2x + 5 into -(2x+5)<x-3<2x+5

-(2x+5)<x-3 x >-2/3

AND x-3<2x+5 x >-8

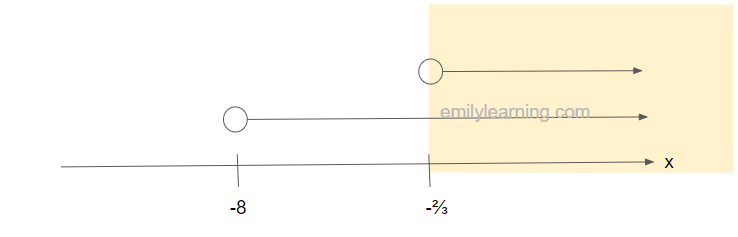
Hence, x > -2/3

Example 2: Solve the inequality |x – 3| ≤ 2x + 5

If given |f(x)| ≤ g(x), split it into -g(x)≤f(x)≤g(x)

Hence, we’ll split |x – 3| ≤ 2x + 5 into -(2x+5)≤x-3≤2x+5

-(2x+5)≤x-3 x ≥-2/3

AND x-3≤2x+5 x ≥-8

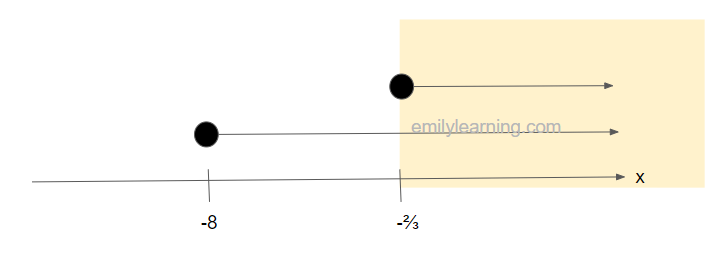
Hence, x≥ -2/3

Example 3: Solve the inequality |x – 3| > 2x + 5

If given |f(x)| > g(x), split it into f(x) > g(x) or f(x) < -g(x)

x-3 > 2x+ 5	OR x-3 < -(2x+5)
x < -8	x < -2/3

We’ll take both (or an inequality that satisfies both answers above), which is x < -2/3

Hence, x< -2/3.

Example 4: Solve the inequality |x – 3| > 2x + 5

If given |f(x)| ≥ g(x), split it into f(x)≥ g(x) or f(x)≤-g(x)

x-3 ≥ 2x+ 5	OR x-3 ≤ -(2x+5)
x ≤ -8	x ≤ -2/3

We’ll take both (or an inequality that satisfies both answers above), which is x ≤ -2/3.

Hence, x≤ -2/3.

---

Learn H2 A Level Math Inequalities

Here are the complete notes for solving inequalities for H2 Math:

• Solving inequalities using the graphic calculator
• Solving inequalities involving polynomials
• Solving inequalities involving polynomial fractions
• Quadratic functions that are always positive or negative
• Solving inequalities with functions that are always positive or negative
• Modulus Functions
• Solving inequalities involving modulus functions 1
• Solving inequalities involving modulus functions 2
• Solving inequalities involving modulus functions 3

All the notes for H2 A Level Math

Go here to find all the notes and resources for H2 A level Math.