Binomial distribution questions are found in paper 2, section B (Statistics section) of the H2 A Level Math exam. In this post, you will find the worked solutions for past A Level questions on binomial distribution.
A list of past questions from each statistics topic can be found here.
A quick summary of formulae in each statistics topics can be found here.
Past A Level Binomial Distribution Questions
These are the past A Level binomial distribution questions for the new syllabus (syllabus 9758) which started from 2017.
Click on the link to go straight to the worked solutions for each question.
Binomial Distribution Question: 2017 Paper 2 Question 9
(i) Assumptions needed for the number of faulty lights in a box to be well modelled by a binomial distribution are:
- The probability that each of this certain brand of kitchen light is faulty is a constant of 0.08.
- The event that one kitchen light (of this certain brand) is faulty is independent of other kitchen lights (of this certain brand).
(ii) Let X be the number of faulty lights out of 12.
X~ B(12, 0.08)
P(X≥1 ) = 1 – P(X = 0) = 0.632333 = 0.632 ( 3 s.f.)
(iii) Let Y be the number of boxes out of 20 with at least one faulty light.
Y~B( 20, 0.632333)
P(Y=20) = 1.04454 x 10-4 = 1.04 x 10-4
(iv) Number of light bulbs in 1 carton = 20 x 12 = 240
Let W be the number of light bulbs that are faulty out of 240.
W~ B(240, 0.08)
P(W≥ 20 ) = 1- P (W ≤ 19) = 0.458333 = 0.458 ( 3 s.f.)
(vi)
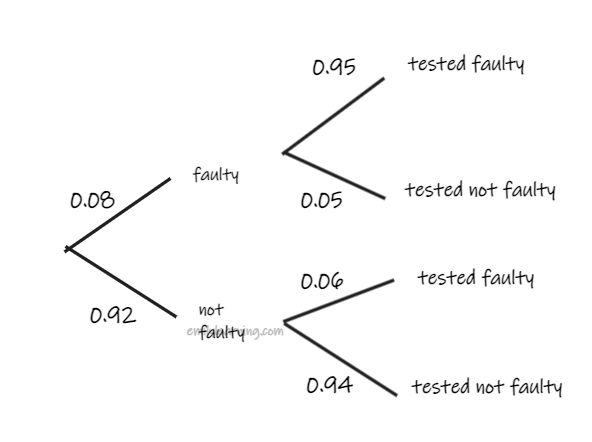
P(not faulty light| identified as faulty)
= P(not faulty and identified as faulty) / P(identified as faulty)
= 0.92 (0.06) /[0.92 x 0.06 + 0.08 x 0.95]
= 0.42073
= 0.421 ( 3 s.f.)
(vii) P(quick test identifies correctly) = 0.08 (0.95) + 0.92(0.94) = 0.9408
(viii) For a light bulb that is identified as faulty, there is a 42.1% chance that it is not faulty. As this probability is relatively high, the quick test may not be worthwhile.
** part (vi) to (viii) are probability questions.
Binomial Distribution Question: 2019 Paper 2 Question 7
(i) Assumptions needed to model F by a binomial distribution are:
- The probability that each mug is faulty is a constant of 0.08.
- The event that a mug is faulty is independent of whether other mugs are faulty.
(ii) F~ B(50, 0.08)
P(F ≥ 7) = 1 – P(F≤ 6) = 0.10187 = 0.102 ( 3 s.f.)
(iii) Let X be the number of days out of 5 where there are at least 7 faulty mugs.
X~ B(5, 0.10187)
P(X ≤ 2) = 0.990978 = 0.991 ( 3 s.f.)
(iv) Let Y be the number of saucers that are faulty out of 10 saucers.
Y~B(10, p)
P(Y =2) = 10C2 p2 (1-p)8 = 45p2 (1-p)8
(v) 2 mugs and 2 saucers are chosen
P(at most 1 faulty item)
= P( all 2 mugs and 2 saucers are not faulty) + P(1 mug is faulty, the rest are not faulty) + P( 1 saucer is faulty and the rest are not faulty)
= 0.922(1-p)2 + 2(0.92)(0.08)(1-p)2 + (2)0.922(p)(1-p)
= 0.97
Using Graphic calculator,
p = 0.06889128 or -0.4899439 (reject since p is probability and will take values between 0 and 1)
p = 0.06889128 = 0.0689 ( 3 s.f.)
Binomial Distribution Question: 2020 Paper 2 Question 9
(i) For the 10 ballpoint pens that are selected (from the 100 ball point pens), each ballpoint pen has an equal chance of being selected.
(ii) Let X be the number of ballpoint pens out of 10 that are faulty.
X~B(10, 0.06)
P(X ≤ 2) = 0.981162 = 0.981 ( 3 s.f.)
(iii) P(box is rejected) = 1 – 0.981162 = 0.018838
Let Y be the number of boxes out of 75 that are rejected.
Y~ B(75, 0.018838)
5% of 75 = 3.75
P(Y> 3.75) = 1- P(Y≤ 3) = 0.0534542 = 0.0535 ( 3 s.f)
(iv) Let W be the number of pens that are faulty out of 5.
W~B( 5, 0.06)
P(W =0) = 0.73390
P(W = 1) = 0.23422
P(W=2) = 0.029901
X~B(10, 0.06) ,
P(X= 0) = 0.53861
P(X ≤ 1) = 0.88241
P(chosen box is accepted)
= P(W =0) + P(W=1)P(X≤ 1) + P(W=2)P(X=0)
=0.95668
= 0.957 ( 3 s.f.)
(v) Less pens is needed for testing ( 5 for the alternative method, compared to 10 for the traditional method). This likely results in a faster test.
Binomial Distribution Question: 2021 Paper 2 Question 11
(a) (i) The supervisor can label each lamp with a number ( e.g. 1, 2, 3, etc.). Then use a computer to randomly generate 100 numbers. The lamps with labels corresponding to the generated number will be used for testing.
(ii) Using the graphic calculator, average number of faulty lights out of 100 tested = 3
p = 3/100 = 0.03
(iii)
Let Y be the number of faulty lamps out of 100. X~B(100, 0.03)
P(Y = 3) = 0.22747 = 0.227 (3 s.f.)
Expected number of days = 150(0.22747) = 34.1205 = 34.1 ( 3 s.f.)
(b)
(i) Assumptions needed for X to be well modelled by a binomial distribution are:
The probability that each heating element is faulty is a constant.
The event that a heating element is faulty is independent of other heating elements.
(ii) X~B(80, 0.02)
P( 1 ≤ X ≤ 4) = P(X≤4) – P(X = 0) = 0.77899 = 0.779 ( 3 s.f.)
(iii) P(X > 3) = 1 – P(X≤3) =0.0768549
Let W be the number of days out of 5 with more than 3 heating elements being faulty.
W~B(5, 0.0768549)
P(Y≥ 2) = 1 – P(Y≤1) = 0.050500 = 0.0505 (3 s.f.)
(iv)
No. of heating elements tested in 5 days = 5 x 80 = 400
Let H be the number of heating elements out of 400 that are faulty.
H~ B(400, 0.02)
P( H≤ 8 ) = 0.592552 = 0.593 (3 s.f)
A Complete Course on H2 A Level Math Statistics
Want a complete course on H2 A Level Math Statistics?
Check out our course here, where we cover all the topics tested in statistics.
The course includes concepts, types of questions, and how to apply them, so that you’ll score for your exam.

