Probability questions are found in paper 2, section B (Statistics section) of the H2 A Level Math exam. In this post, you will find the worked solutions for past A Level questions on probability.
A list of past questions from each statistics topic can be found here.
A quick summary of formulae in each statistics topics can be found here.
Past A Level Probability Questions
These are the past A Level probability questions for the new syllabus (syllabus 9758) which started from 2017.
Click on the link to go straight to the worked solutions for each question.
2017 Paper 2 Question 9 (vi) to (viii)
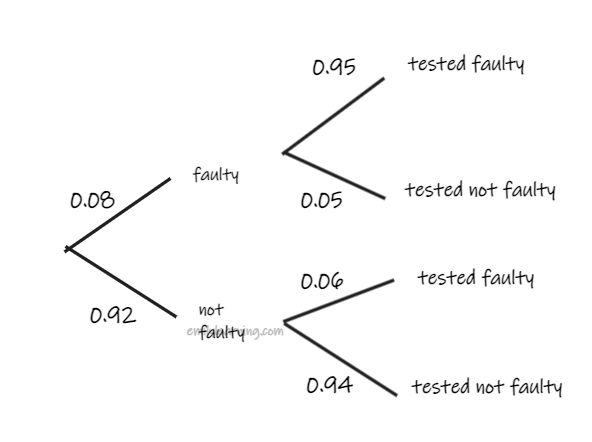
Probability Question: 2017 Paper 2 Question 9 (vi) to (viii)
(vi)
Probability Question: 2018 Paper 2 Question 6
(i) By observation, it’s observed that no matter which route is taken to reach D, it involves 8 steps, 3 of them are right fork and 5 of them are left fork.
Probability that bug finishes at D = 8! / (3!5!) p5q3 = 56p5q3 [shown]
(ii) Let X be the number of left forks made out of 8. X~B(8, p)
Given probability at D = P(X= 5) is maximum for this binomial distribution,
we know that P(X =5) > P(X =6) and P(X= 5) > P(X=4)
56p5(1-p)3 >8C6 p6(1-p)2
56p5(1-p)3 > 28p6(1-p)2
2(1-p)- p > 0
2-3p > 0
p<2/3
and
56p5(1-p)3 >8C4 p4(1-p)4
56p5(1-p)3 >70p4(1-p)4
4p – 5(1-p) > 0
p>5/9
Hence 5/9 <p <2/3
(iii) To reach any endpoint at A- I, bug will take 8 moves.
In each move, probability that bug is not swallowed by black hole = 1 – 0.1 = 0.9
To reach A-I without being swallowed by black hole, for all 8 moves, bug must not be swallowed by black hole.
Required probability = (0.9)8 = 0.43046721
Note: This question can be done as a binomial distribution. Part (ii) is testing students on mode of binomial distribution.
Probability Question: 2018 Paper 2 Question 7
This probability question is best down using either formulae and/ or sketching of Venn diagrams.
(i) Since A and B are independent, P(A∩B) = P(A) x P(B) = ab
P(A’∩B’) = 1 – P(AUB) = 1- [a + b – ab] = 1- a-b+ ab
P(A’) = 1- a; P(B’) = 1 -b
P(A’)xP(B’) = (1-a)(1-b) = 1-a-b+ab = P(A’∩B’)
Since P(A’) x P(B’) = P(A’∩B’), A’ and B’ are independent events. [shown]
(ii) Since A and C are mutually exclusive, P(A∩C) = 0
P(A’∩C’) = 1 – a – c
(iii) Given A’ and C’ are not mutually exclusive,
based on information from the first part, P(A) and P(B) are independent –> P(A)P(B) = P(A∩B)
max P(A∩B) = 2/15
min P(A∩B) = 1/3
Probability Question: 2019 Paper 2 Question 8
(i) (a) Required probability = (9+ 14)/56 = 23/ 56
(b) Required probability = (11+15)/56 = 13/ 28
(ii) (a) Required probability = 8/56 x 7/ 55 = 1/55
(b)
Case 1: yellow dog + not dog and not yellow
Probability for case 1 = 7/56 x (8+13+11)/55 x 2 = 8/55
Case 2: Non- yellow dog + yellow non dog
Probability for case 2 = 10/56 x 7/55 x 2 = 1/22
Total probability = 1/22 + 8/55 = 21/110
(iii) probability of selecting the 2 combination = 1/77 = (2 x 20)/(56 x 55)
20 = 5 x 4
Possible combinations are:
- white horse and white rider
- white horse and yellow bird
- orange bird and yellow bird
- orange bird and white rider
Probability Question: 2020 Paper 2 Question 8
(i)No. of ways to choose 12 shapes = 28C12 = 30 421 755
No. of ways to choose 1 rectangle and 11 circle = 17C1x 11C11= 17
No. of ways to choose 2 rectangles and 10 circles = 17C2x 11C10= 1496
P(R = 1) = 17/ 30 421 755
P(R = 2) = 1496/ 30 421 755 > P(R= 1)
Hence P(R= 1) < P(R=2)
(ii) 11 circles and (17+r) rectangles
Let total number of ways to choose 12 shapes from 11 circles and (17+r) rectangles be n.
No. of ways to choose 4 rectangles and 8 circles = 17+rC4 x 11C8= 165(17+rC4 )
No. of ways to choose 3 rectangles and 9 circles = 17+rC3 x 11C9 = 55(17+rC4 )
Given 165(17+rC4 )/ n = 15[ 55(17+rC3 )/ n]
17+rC4 = 5[17+rC3]
(17+r)!/ [4!(13+r)!] = 5[(17+r)!/(3!(14+r)!)]
1/ [4(13+r)!] = 5/ [(13+r)!(14+r)]
1/4 = 5/ (14+r)
r = 6
Probability Question: 2021 Paper 2 Question 7c
(a) No. of ways = 11! / (5! 2! 2!) = 83 160
(b) No fo ways = 4! (3)(2!) = 144
(c) Probability = [7!/ (2! 2!)] / 83 160 = 1/ 66
Note: part (a) and (b) are permutation and combination question, while part (c) is a permutation and combination cum probability question.
A Complete Course on H2 A Level Math Statistics
Want a complete course on H2 A Level Math Statistics?
Check out our course here, where we cover all the topics tested in statistics.
The course includes concepts, types of questions, and how to apply them, so that you’ll score for your exam.

