Summary Notes for Differentiation and its Application – O Level Add Math

There’s quite a number of concepts tested for differentiation and its application. In fact, this is the largest topic in O Level Additional Mathematics. We talked about what’s in the syllabus for differentiation and its in this post here. In this post, let’s summarize the concepts from these topics of differentiation.

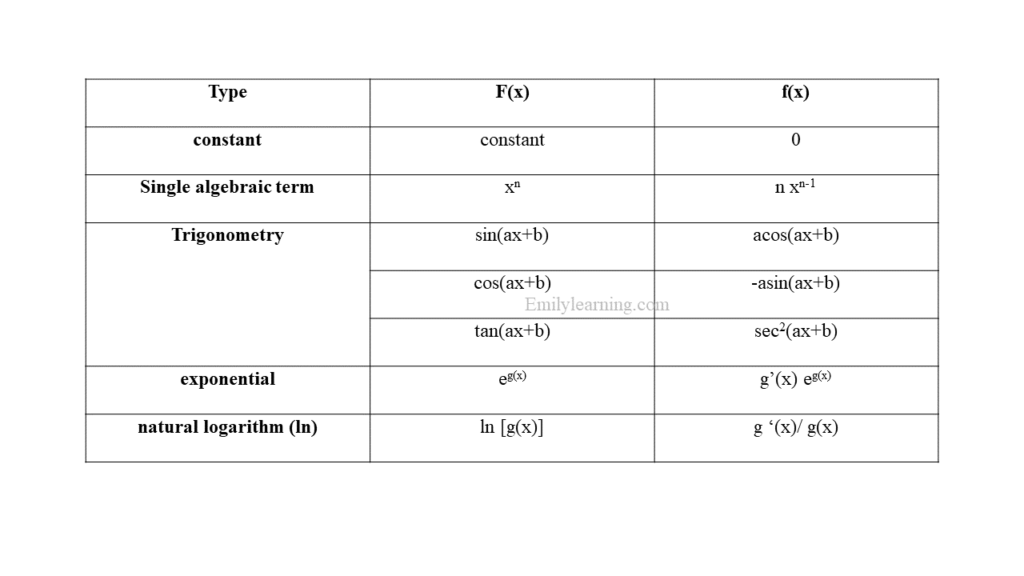
Differentiation Formula

These are the basic formulae that you should know for O Level Add Math differentiation. As they are not in the formula booklet, make use you remember them!

Chain rule, Product Rule and Quotient Rule in Differentiation

Chain Rule

• Use the chain rule if you only have one group of expression with a power

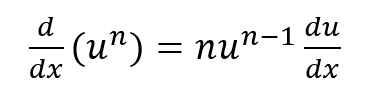
, where u is an expression in terms of x.

Product Rule

• When you have 2 groups of expressions (e.g. u and v) multiplied with each other, use product rule for differentiation.
• Product rule formula:

 where u and v are expressions in terms of x

• When using product rule, remember to simplify your expression by factorization. I go through how to do this in my on-demand A- Math course here. 

Quotient Rule

• When you have 1 expression divided by another, use quotient rule for differentiation. where u and v are expressions in terms of x.
• You can also change the power of the denominator to a negative one, and use product rule for differentiation. See example below:

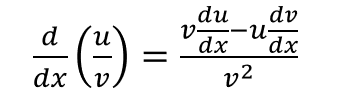
where u and v are expressions in terms of x

First Derivative, Second Derivative, and so on

Assuming that we have a function y = f(x), when we differentiate it, we are finding the first derivative of y or dy/dx.

• First derivative = dy/dx
• Second derivative (d²y/ dx²)
  • When you differentiate the first derivative, you get the second derivative or d²y/ dx²
• third derivative (d³y/ dx³)
  • When you differentiate the second derivative, you get the third derivative or d³y/ dx³

Increasing and decreasing functions and Differentiation

• Increasing functions: dy/dx > 0
• Decreasing functions: dy/dx < 0

Tangents and Normals 

• Gradient of tangent at P = dy/dx at the point P
• Gradient of normal = -1/ (gradient of tangent)

Rate of change and chain rule

• Example of chain rule: dy/dt = (dy/dx)(dx/dt) 

Stationary Points / Maximum ,  Minimum and Point of Inflexion

• Maximum points, minimum points and points of inflexion are stationary points. At these points, dy/dx = 0.
• Maximum point:
  • second derivative < 0
• Minimum point:
  • second derivative > 0
• Point of inflexion:
  • second derivative =  0 (there is no change in sign of the first derivative slightly before or slightly after that point of inflexion)

Mathematics is all about applying and being able to do questions. Apart from knowing these notes and formulae, you must also be familiar with how to apply them to the questions. The nice thing about Additional Mathematics is the questions are quite standard.

Want a systematic method to approach O Level Additional Mathematics questions? Check out our course here.