What is a geometric progression
A geometric progression (GP) is one in which the ratio (r) between any 2 consecutive terms is a constant.
Examples of geometric progression
An geometric progression is one where the ratio between any 2 consecutive terms is a constant. This ratio can be a positive or negative difference. Examples of arithmetic progressions are:
- 2, 4, 8, 16, 32, 64….. In this example here, the first term is 2, and to get to the next term, we multiply it by 2. We call 2 the common ratio of this geometric progression.
- 20, -10, 5, -2.5, …… In this example here, the first term is 20, and to get to the next term, we multiply it by -0.5. We call -0.5 the common ratio of this geometric progression.
General Expression for nth term and sum of first n terms
If a is the first term, and r is the common ratio of an geometric progression,
nth term, uₙ = arⁿ⁻¹
Sum of first n terms, Sₙ is given by:
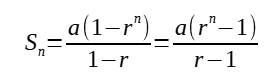
How to prove a sequence is a geometric progression?
Since a geometric progression is one where the ratio between 2 consecutive terms is a constant, to prove an geometric progression, you’ll need to prove that uₙ/uₙ₋₁ = constant.
Sum to infinity of a geometric progression
When |r| < 1, as n →∞, uₙ → 0.
Hence, a geometric progression is convergent only when |r| < 1. When that happens, a sum to infinity exists, and the sum to infinity, S∞ is given by:
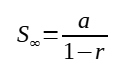
Sequences and series, AP& GP, and summation notes
- Sequences and series
- Arithmetic progression
- Geometric Progression
- Using the Graphic calculator (Ti84) for AP & GP Questions
- Summation: Introduction
- Finding summation using the graphic calculator
- Method of difference and summation
All the notes for H2 A Level Math
Go here to find all the notes and resources for H2 A level Math.
