Imaginary number i
i is an imaginary number, where i = √(-1).
Since i = √(-1), i² = -1.
Ways to represent complex numbers
Complex numbers consist of both the imaginary and the real portion. We can represent complex numbers in :
- cartesian from i.e. x + iy
- exponential form:
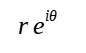
- trigonometric form i.e. r(cosθ + i sinθ)
Representing a complex number on the argand diagram
For a complex number, in cartesian from e.g. z = x + iy, x refers to its x coordinate, and y refers to its y coordinate.

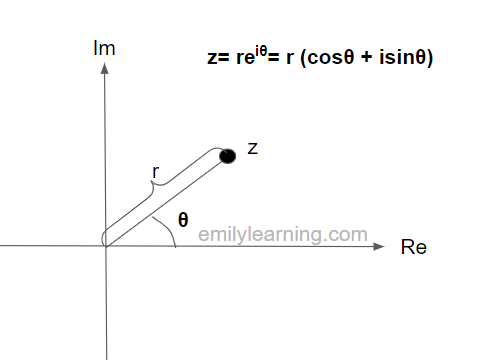
For a complex number in exponential or trigonometric form, we use r and θ to locate the complex number on the argand diagram. r and θ refers to:
- r is the length between the origin and the complex number on the argand diagram
- θ is the angle the complex number makes with the positive x- axis (or real axis)
Modulus Argument Form
For a complex number z, it can be written as z = x + iy
|z| = r= √(x² +y²)
θ = arg(z) = the angle z makes with the positive x-axis in the argand diagram, where -𝞹<arg(z)≤𝞹
Some Useful Results
|z₁z₂| = |z₁||z₂|
arg(z₁z₂) = arg(z₁)+arg(z₂)
|z₁/z₂| = |z₁|/|z₂|
arg(z₁/z₂) = arg(z₁)-arg(z₂)
|z₁ⁿ| =|z₁|ⁿ
arg(z₁ⁿ) = n arg(z₁)
Conjugate
We use the symbol * to denote conjugate of a complex. For instance, the conjugate of the complex number z, can be written as z*.
Finding conjugate of a complex number in cartesian form
If z = x + iy, then its conjugate, z* = x – iy.
Finding conjugate of a complex number in trigonometric or exponential form
If |z| = r, and arg(z) = θ, then for the conjugate of z, i.e. z*:
|z*| = r
arg(z*) = -θ
Solving Equations involving complex roots
If all the coefficients are real, then the complex roots occur in conjugate pairs.
