Summary Notes for Coordinate Geometry, Circles and Proof in Plane Geometry – O Level Add Math

Here, you will find the summary notes for coordinate geometry, circles, and proof in plane geometry written based on O Level Additional Mathematics Syllabus.

We talked about what’s in the syllabus for these topics in the article here. Most of what’s covered in these topics are also covered in the Mathematics syllabus for O Level, so do revise, or at least memorize the formulae in Mathematics when you are revising O Level Additional Mathematics.

In my course on O Level Additional Mathematics, I’ll go through all the essential formulae that you’ll need to know for O Level Add Maths (including those that are already covered in elementary mathematics). You can get my course here.

Coordinate Geometry

For coordinate geometry, know these formulae:

Straight Lines

• Equation of straight line: y = mx +c
  • m is the gradient
  • c is the y- intercept 
• Parallel lines have the same gradient
• For 2 lines that are perpendicular to each other, multiplication of the gradients will give -1.
• For 2 points (x1, y1) and (x2, y2), gradient of line is given by:
  • gradient = (y1- y2)/ (x1 – x2)

Distance between 2 points

For points A (x1, y1) and B (x2, y2), the distance of AB is given by:

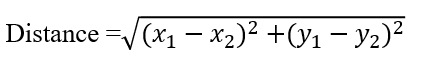
Midpoint

For points A (x1, y1) and B (x2, y2), the midpoint of AB is given by:

Finding area

To find the area, use the shoelace method. Let’s use this diagram below as an example to illustrate the shoelace method:

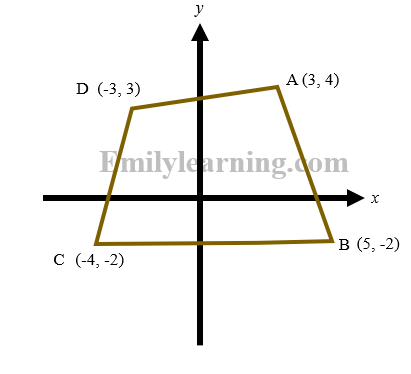
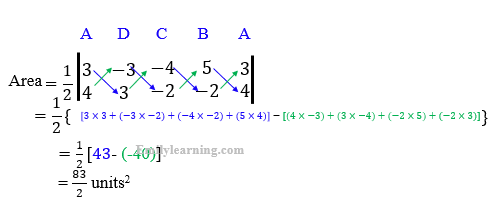
Area of the quadrilateral ABCD can be found by shoelace method:

Coordinate Geometry for Circles

There are 2 ways to express the general equation of a circle:

• (x-a)²+ (y-b)² =r² 
  • radius of circle = r units;
  • centre of circle is (a, b)
• x² + y²+ 2gx + 2fy +c = 0

Proofs in Plane Geometry

Here, you’ll need to prove similar triangles and/ or congruent triangles. From past questions, the use of AAA or proving that 2 pairs of angles in the 2 similar triangles are the same (and hence the third angle will be the same) is the most commonly used proof for O Level Additional Mathematics.  Many questions also involve circles, so you will need to make use of the concepts learnt in properties of circles in this chapter for Additional Mathematics. While questions involving circles for geometry questions in elementary mathematics mainly ask you to find the angle, in O Level Additional Mathematics, you are asked to proof (e.g. angle ABC = angle EFG and so on).
There aren’t many new concepts for this chapter (apart from the different ways in which questions are asked). New concepts here include:

• alternate segment theorem

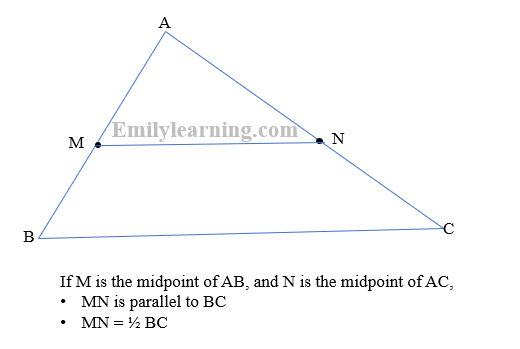
• mid-point theorem

What’s next after knowing the concepts?  Apply them!

Want to learn O Level Add Maths on-demand?

Knowing the concepts and formulae above is not enough for you to even pass the O Level Additional Mathematics exams. You need to know how to apply these concepts. So, you’ll definitely need to try questions. 

In our course on O Level Additional Mathematics, we’ll go through the types of questions that are asked in each topic, what concepts are tested, and how to apply them. With these skills, students finish the course as confident students, able to apply what they have learned to tests and exams. If you want to ace these chapters in Additional Mathematics, definitely check out O Level Additional Mathematics Course here.