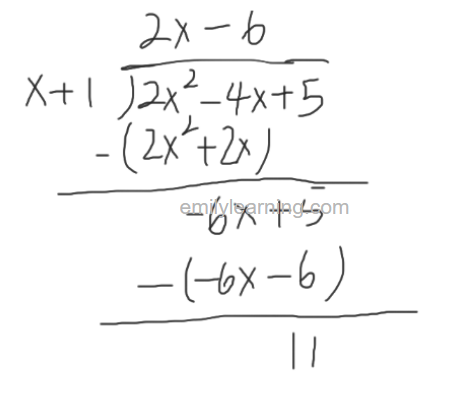Sketching the graph of y = (ax²+bx+c)/(dx+e)

The graph of y = (ax² + bx + c) / (dx+e) has the following:

• vertical asymptote at x = -e/d
• oblique asymptote of y = mx + n –> where mx + n is the quotient when ax² + bx + c is divided by dx +e

Deriving the asymptotes:

The asymptotes can be derived by the following way:

• vertical asymptote is when denominator is equal to 0 –> dx+e = 0, x = -e/d
• oblique asymptote occurs when x→±∞:

Sketching the graph of y = (ax²+bx+c)/(dx+e)

The graph of y = (ax²+bx+c)/(dx+e) can be sketched using the Ti-84 graphic calculator. To do so:

Step 1: Press [y=]

Step 2: Type in the equation

Step 3: Press [graph]

Note that equation of asymptotes are not shown on the graphic calculator.

Examples of sketching the graph of y = (ax²+bx+c)/(dx+e)

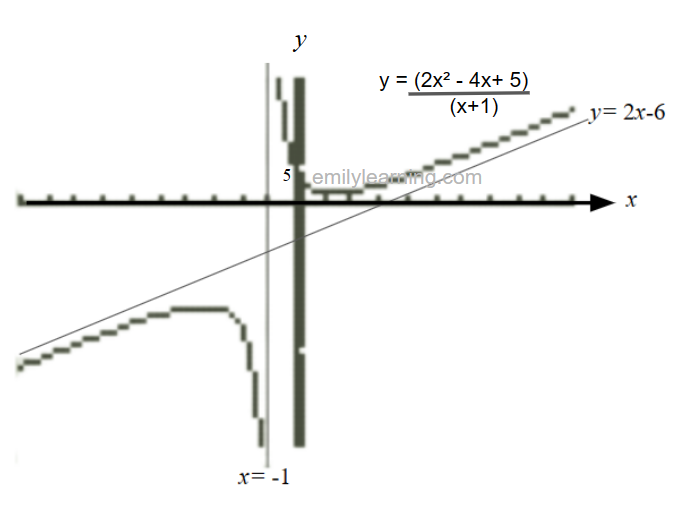
Example: Sketch the graph y = (2x² – 4x+ 5)/ (x+1)

• Vertical asymptote: x = -1
• To obtain the oblique asymptote, we do a long division for 2x² – 4x+ 5 divided by x+1. The quotient gives the equation of the oblique asmyptote.
  • Hence, oblique asymptote is y = 2x-6