A sample refers to a subset of a larger population or data set. The purpose of sampling is to gather information about the population by studying a smaller and more manageable portion of it, rather than attempting to examine the entire population, which can often be impractical or time-consuming. By analyzing the sample, we can make inferences and draw conclusions about the characteristics of the entire population.
Types of samples
Random Sample:
In a random sample, each individual element in the population has an equal chance of being selected.
Stratified Sample:
In a stratified sample, the population is divided into subgroups or strata based on some characteristic (e.g., age, gender, location). Then, a random sample is taken from each stratum. Stratified sampling is often used when the population has distinct subgroups, and researchers want to ensure representation from each group.
Systematic Sample:
In a systematic sample, elements are selected at regular intervals from a list of the population. For example, every 10th person from a list may be included in the sample. Systematic sampling can be more convenient than simple random sampling when a complete list of the population is available.
Convenience Sample:
A convenience sample is a non-probabilistic sampling method where the researcher selects the individuals or elements that are most easily accessible or convenient. Convenience sampling is not considered representative and may introduce bias, but it can be useful for exploratory research or when other sampling methods are impractical.
Cluster Sample:
In a cluster sample, the population is divided into clusters (e.g., geographical areas), and a random sample of clusters is selected. Then, all individuals within the selected clusters are included in the sample. Cluster sampling can be more efficient when it is difficult to create a complete list of the population.
Judgment Sample:
In a judgment sample, the researcher uses their judgment or expertise to select individuals for the sample. This method is subjective and may introduce bias, but it is sometimes used when the researcher believes certain individuals are critical to the study.
Central Limit Theorem
If x̄ represents mean of X out of n samples, where n is large, if the distribution of X is unknown, or the distribution is NOT a normal distribution, we can still say x̄ ~ N( μ, σ2/ n), by Central Limit Theorem.
Common Formulae used in Sampling
- unbiased estimate of population mean = μ = Σx/ n
- unbiased estimate of population variance = s2 , where the formulae for s2 can be obtained from your data booklet
- relationship between sample variance (σ2) and unbiased estimate of population variance (s2):
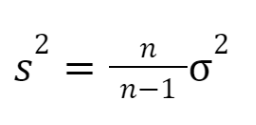
How to approach H2 A Level Math Statistics Questions
Want a complete course on sampling, and the ENTIRE OF H2 A Level Math Statistics?
Check out our course here, where we cover all the topics tested in statistics.
The course includes concepts, types of questions, and how to apply them, so that you’ll score for your exam.
