Summary Notes for Integration and its Application – O Level Add Math

Here, you’ll find the summary notes for integration and application of integration written based on what’s tested in the O Level Add Maths syllabus. In my previous articles, I talked about what you need to know about integration and its application for O Levels. You can read about what’s tested for integration and its application in detail here. 

Integration formulae tested in O Level Additional Mathematics

• integration of constant ; ∫ a dx = ax + c
• integration of single algebraic term where the power, n is not -1: ∫ axⁿ dx = (axⁿ⁺¹)/(n+1) + c 
• integration of (ax+b)ⁿ where the power of n is not -1: ∫ (ax+b)ⁿ dx = (ax+b)ⁿ⁺¹/[a(n+1)] + c
• integration of trigonometric functions:
  • ∫ sin(ax+b) dx = – [cos(ax+b)]/a + c
  • ∫ cos(ax+b) dx =  [sin(ax+b)]/a + c
  • ∫ sec²(ax+b) dx =  [tan(ax+b)]/a + c
• integration of exponential functions:
  •     ∫ e^ax+b dx =(e^ax+b)/a + c
• integration of algebraic terms with power of -1:
  • ∫ 1/x dx = lnx + c
  • ∫ 1/(ax+b) dx = (1/a)ln(ax+b) + c

Definite integral vs indefinite integral

• Definite integral i.e. ∫^b_af(x) dx
  • You’ll get a constant after integrating.
  • ∫^b_af(x) dx =F(b) – F(a)
• Indefinite integral: 
  • You’ll get an expression with an arbitrary constant (usually denoted as c) after integrating.
  • ∫^b_af(x) dx = F(x) + c

Integration as the reverse of differentiation

You also need to know how to apply the knowledge of integration as the reverse of differentiation. Meaning, if you differentiate f(x) and get f'(x), then when you integrate f'(x), you will get f(x) +c.
d/dx[f(x)] = f ‘(x)    <—->      ∫f ‘(x) dx = f(x) + c

Finding the area under the curve by integration

The area bounded by the curve y= f(x), the x- axis, x = a and x =  b based on the diagram below is given by ∫^b_af(x) dx.

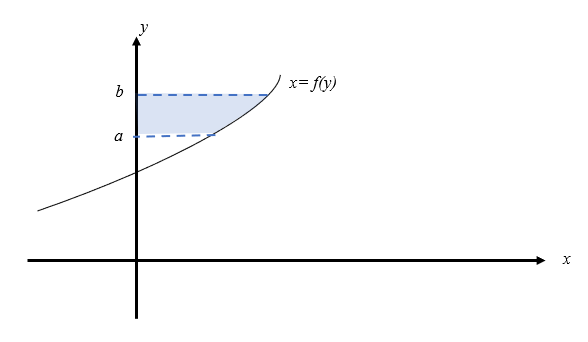
The area bounded by the curve x= f(y), the y- axis, y = a and y =  b based on the diagram below is given by ∫^b_af(y) dy.

Finding the area between two curves

The area bounded by the curve y = f(x) and y = g(x) based on the diagram below is given by  ∫^b_a [g(x) – f(x)]dx.

The area bounded by the curve x = f(y) and x = g(y) based on the diagram below is given by  ∫^b_a [g(y) – f(y)]dy.

Mathematics is all about applying and being able to do questions. Apart from knowing these notes and formulae, you must also be familiar with how to apply them to the questions. The nice thing about Additional Mathematics is the questions are quite standard.

In my O Level Additional Mathematics course, I go into detail not only the concepts but how to apply them. We also go through many questions together step-by-step, so that students finish the course equipped with the skills needed to tackle their tests and exams. You can purchase the course instantly here.

Here’s a visual summary of integration and its application: